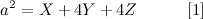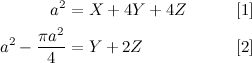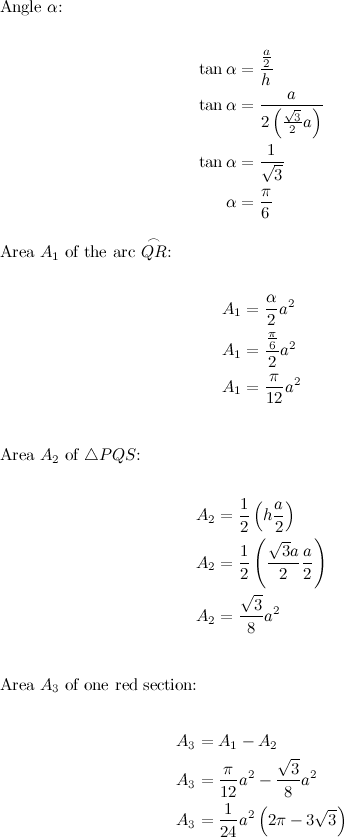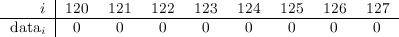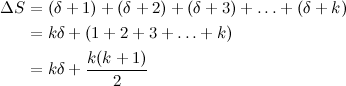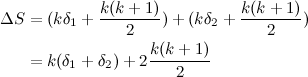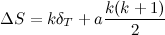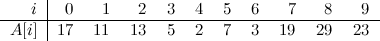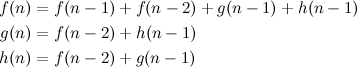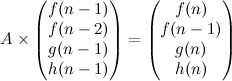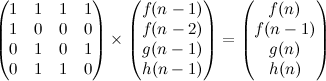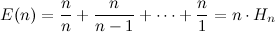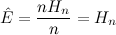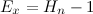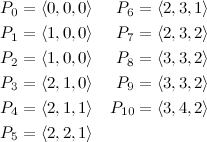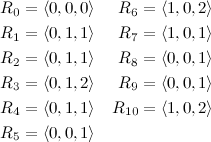Is This Integration?

Problem Name: Is This Integration?
UVa ID: 10209
Keywords: geometry, math

I’ve been meaning to write about a geometry problem for a while now, because they generally provide interesting challenges that require some degree of creativity. With some types of problems, you can sometimes formulate your solution almost immediately after reading the problem statement. When you tackle a geometry–related problem, however, it’s rare that you can come up with a solution without doing at least some amount of mental work out first.

This problems asks us to consider a geometric figure built as follows: start with a square with sides of length \(a\). Now draw four arcs of radius \(a\) and angle \(\pi \div 2\), with their centers in each of the four corners of the square, and draw these arcs so they all lie inside the square. This produces a figure like this:

As you can see, the area of the square gets divided into 9 different sections of three different kinds, labeled here as \(X, Y, Z\). We’re asked to calculate the total area covered by these three types of sections —that is, the values \(X, 4Y, 4Z\).

Now, there’s probably many ways to get to the answer, but let’s try building our own, step by step. First of all, we can observe that we need to deduce the values of three unknowns (\(X\), \(Y\) and \(Z\)), so by simple algebraic reasoning, we can be sure that we need at least three independent equations to solve these unknowns.

Let’s start with what is probably the easiest equation to derive from the figure: the total area of the square must be equal to the sum of the areas from all 9 sections:

This first equation is based on the area of the square, but we did not consider the arcs, so let’s do that for the second equation. Let’s consider the coloured area in the following figure:

We can observe here that the given section is equal to the area of the square minus the area of one quarter of a circle of radius \(a\):

It seems that we’re making good progress. We just need one more equation. However, at this point it’s easy to come up with something that looks new, but isn’t. For example, let’s say that we wanted to formulate a new equation for the area of the following section:

The problem is that, no matter how we look at it, the equation that we can derive from this is going to be basically the same as equation [2] above (try it!). If we analyse this for a moment, it shouldn’t be a surprise: we’re producing relations from the same elements (the square and the arcs). What we need is a completely new geometric element to use as a base for our last equation.

Let’s stop for a moment then, and take a look at our first figure, and ask ourselves: what other interesting (the word critical may come to mind) elements can we recognise in there? We have tried with the lines —either the straight lines from the square, or the curved lines from the arcs—, but what about the points? Maybe the intersection points can give us something useful. For example, let’s consider the following section of the figure:

With some geometric reasoning, and a little algebra, we could derive a new equation to solve the value \(Z\). First of all, let’s find the height \(h\) at which the two relevant arcs intersect and which marks one of the sides of the coloured rectangle from the last figure.

Starting from the standard equation of a circle with radius \(a\), and given that the symmetry shows that the intersection point happens horizontally right in the middle of the square, we can deduce \(h\) like this:

Now, if we knew the area covered by the red sections, then the value of \(Z\) could be easily deduced. So let’s see what else we can find out from our last figure:

We can observe now that the one of the red sections has an area equal to the area of the arc \(\stackrel\frown{QR}\) minus the area of \(\triangle PQS\). And we can calculate these areas by knowing the angle \(\alpha\) and the sides of the triangle \(\triangle PQS\) which are \(h\) and \(a \div 2\):

With all of this, we can finally summarise our findings with the three equation we were looking for:

The corroboration of equation [3] and deducing the final values of \(X\), \(4Y\) and \(4Z\) is left as an exercise to the reader :). Also, try perhaps looking for a simpler way to deduce all of these values. As I said before, there’s usually more than one way to do it, and some can be simpler than others. By simply staring at the original figure for a little while, an interesting idea may pop up in your head that helps you solve this in a way that you find easier to understand. And you’ll never know unless you try :).

Rip Van Winkle's Code

Problem Name: Rip Van Winkle’s Code
UVa ID: 12436
LightOJ ID: 1411
Keywords: segment tree, lazy propagation

Today we’ll take a look at a problem from this year’s ACM ICPC World Finals Warmup contest, and which can be solved with the help of segment trees. It will give us an opportunity to contemplate some more of the nice subtleties that often come into play in this type of problem.

We’re asked to consider an array of 64–bit integers. The size of this array is fixed at 250,001 positions (index 0 is left unused, so we have to focus only on positions 1–250,000) and it is initially filled with zeroes. Three types of operations can modify this array:

• Operation A takes two integers, let’s call them \(i\) and \(j\), and adds 1 to position \(i\) of the array, 2 to position \(i+1\), 3 to \(i+2\) and so on. In other words, it increases the values in the range \([i:j]\) of the array according to the sequence \(1, 2, 3, \ldots, (j-i+1)\) from left to right.
• Operation B is similar to A, but it applies the additions in a right–to–left fashion (it adds 1 to position \(j\), 2 to position \(j-1\) and so on).
• Operation C is simpler. It also takes two integers that describe a range, but it receives an extra argument; an integer \(x\). All positions in the range \([i:j]\) of the array are then set to \(x\).

Finally, we have a fourth operation S which doesn’t alter the array, it must simply report the sum of all positions in a given range \([i:j]\) of the array.

Let’s quickly illustrate these operations with an example. We’ll consider the arbitrary range \([120:127]\) of the array. At first, this range looks like this:

Now, let’s say that we receive the following commands to execute in order:

• A 123 126
• A 122 124
• B 120 127
• C 125 127 3

Then the changes inside the data array would look as follows:

Okay, now that we’re a bit more familiar with the problem, let’s give it some thought. As I mentioned in the beginning, we’ll base our approach on the powerful segment tree data structure. With this in mind, it would seem that implementing operations C and S could be fairly straightforward. However, operations A and B are somewhat tricky. They modify a range of values, but each position in that range is modified differently. We should, however, try to implement those commands in a way that involves just one update on the tree (with complexity \(O(\log{N})\)), otherwise our code wouldn’t be too efficient.

Let’s start by visualising our segment tree for the small range we chose in our example. We’ll start with the basics, just storing in each node of the tree the total sum of the corresponding range. We’ll extend this tree gradually as we see fit.

This tree represents the range \([120:127]\) of a fresh array, so it’s filled with zeroes. The first row in each node contains its index and range, while the second row contains the sum of all positions in the corresponding segment in the array. Notice that the nodes of this tree have been indexed using the numbers \(1, 2, \ldots, 15\), but in reality these nodes would receive different indices —node 1 would be for the real root of the tree, which covers the range \([1:250,000]\), node 2 would be its left node, and so on. Numbers 1 to 15 are used here just to simplify things a bit in the following examples, but keep in mind that they would not be the real indices in the segment tree for the whole array.

Alright, let’s consider our first query: A 123 126. How would the tree be affected by this command? We could produce something that looks like this at first:

By looking at this tree, a few things are brought to our attention. One is that the value of each affected node is increased according to a sequence of consecutive integers, but the sequence is of course different for each node. For example, node 6 was increased by 5, which is the result of \(2+3\). For that node, the sequence applied to increase the values in the range \([124:125]\) started with 2, and its length is 2 of course. Another important thing that this graph seems to “shout” at us, is that we must devise a strategy for the propagation of this update. The situation is pretty evident in nodes 12 and 13. How can we tag these nodes so they are properly updated down the road?

But let’s pause for a second and think on the situation of sequences of consecutive integers that start with an arbitrary number. We’ll generalise and consider a node that represents a segment of length \(k\). The contents of the node (the sum of all values in its range) will be denoted \(S\). When we receive an A operation that affects this node, we have to change its contents according to a sum of the form:

Where \(\delta\) represents the distance of each element in the base sequence \(1, 2, 3, \ldots, k\) to the corresponding element in the actual sequence applied to the node, which could start with any positive integer. To illustrate this, we can see in the graph above that, for node 11, \(k=1, \delta=0\); for node 6, \(k=2, \delta=1\); and for node 14, \(k=1, \delta=3\).

This method of representing the A operation has also the benefit of working out nicely when we accumulate the results from more than one command of this type for the same node. The value of \(k\) remains the same in each node, so the only thing that could change is \(\delta\). Let’s say that a certain node receives two A operations, one after the other, with two values \(\delta_1\) and \(\delta_2\). This would result in the following:

In general, if a node receives \(a\) operations of type A, with a total \(\delta_T\) —the result of adding \(\delta_1, \delta_2, \ldots, \delta_a\)— then all these changes can be represented by the expression:

And what about the B operation? Well, if you think about it for a minute, it should be easy to notice that it works very similarly to an A operation. The difference is that the \(\delta\) values are calculated differently (right to left) and that, in order to facilitate the calculation of \(\delta\) values for children nodes, it would be convenient to keep track of the number of B operations with a different variable (let’s call it \(b\)).

Putting all of this together, we can now extend each node of the segment tree with three additional values: \(a\) (the number of A operations to propagate), \(b\) (the number of B operations to propagate), and \(\delta\) (the sum of all \(\delta\) values from either A or B operations). Let’s see how our tree looks like now:

What is nice about this approach is that, given that every node is implicitly associated with a given range of the array, it is easy to determine the values of \(k\) and \(\delta\) in each node (and their children) for every A and B operation. And calculating the new \(S\) from \(a\), \(b\) and \(\delta\) is even easier.

Let’s quickly review how the tree changes with the rest of the operations we used in our original example. After the operation A 122 124 we would have:

And after B 120 127:

Note that, as I mentioned in the analysis of Ahoy, Pirates!, there are some things that happen behind the curtains while propagating updates down the tree. For example, when the second A operation is issued, the tree is traversed down to node number 12, and in the process node 6 and its children are visited, and that’s when node 13 is updated so its \(S\) value becomes 3, while \(a, b, \delta\) are cleared.

Now we have only one operation left to implement: C. We could try to implement it using the \(\delta\) field we have already defined, but that would represent some difficulties when several commands are stacked for future lazy propagation. Consider for example a C command followed by an A operation and vice–versa. To avoid these issues, and for commodity, we’ll simply create a couple of new fields: one boolean field \(c\) that represents whether a C operation is pending or not, and a field \(x\), which is simply the argument for the corresponding C operation.

Let’s see this new extended tree, and how it would change after the command C 125 127 3:

Once again, a few nodes have changed purely as a side–effect of traversing the tree (e.g. nodes 2, 4 and 5). It’s also worth mentioning that once a C operation is passed on to a child node for lazy propagation, the \(a\), \(b\) and \(\delta\) fields of the child are cleared, because the C operation overrides any previous commands. This can be seen, for example, in nodes 14 and 15. However, A and B do not override previous commands.

---

Okay, we have reached the end of this analysis. I’d like to end by commenting on something that I realised while working on this problem, which is that I’ve developed a special appreciation for algorithm problems related to segment trees, because they typically require a little bit of… I guess you could call it “inspiration”, to nail the right representation of the relevant data and to imagine how every operation should work and be propagated through the tree. Not only that, these problems also demand a lot of attention to detail in the implementation, because with so many subtle things to keep track of, it’s easy to make a mistake somewhere.

How nice it is that we all have the opportunity to sharpen our skills by working on fun problems like this one :).

All Possible Increasing Subsequences

Problem Name: All Possible Increasing Subsequences
LightOJ ID: 1085
Keywords: sorting, binary indexed tree

Continuing with my plan to write about data structures I have recently discovered, I’ll talk about a problem that can be solved with the help of a binary indexed tree. But we’ll get to that in a moment; let’s focus on the problem first.

In this problem we’re asked to consider sequences of integers. An increasing subsequence is simply an arbitrary subset of integers from the original sequence, kept in the same relative order, such that the numbers in the subsequence are in strictly ascending order. Putting it into more formal terms, let \(A\) be an array of \(N\) integers (indexed from zero to \(N-1\)). Then an increasing subsequence of length \(k\) can be described by a list of indices \(s_1, s_2, \ldots, s_k\) such that \(0 \leq s_1 < s_2 < \ldots < s_k < N\) and \(A[s_1] < A[s_2] < \ldots < A[s_k]\). Note that a subsequence can be of length one, which means that any number in \(A\) by itself forms an increasing subsequence.

The problem consists of finding the total number of increasing subsequences that can be found in a given sequence of integers. Let’s get our hands dirty with a simple example, which is always helpful to wrap our heads around problems and their solutions.

Here we have an array \(A\) of 10 elements, all distinct integers (pretty integers, by the way). At this point, you can try to find out the number of increasing subsequences in \(A\) by yourself, if you feel inclined to do so.

If you haven’t figured out a way to solve it yet, I recommend you give it a try, at least for a few minutes. It is important to spend the time doing that mental workout. Here’s a little hint, before I blurt out the strategy I have in mind: think about going step by step, in order.

Okay, here’s how the process might look like for this example. Hopefully it will help you get a grip on the core of the algorithm we’re going to use. We’ll take elements from the original sequence, one by one and in ascending order, and find out the number of increasing subsequences (ISS) we have found so far at each step:

A few steps have been left out (try to complete the list), but did you get the gist of it? Let’s put it into words:

• Let \(S\) be an array of length \(N\), where \(S[i]\) will represent the number of increasing subsequences that end at position \(i\) (so the last number of those subsequences would be \(A[i]\)). Initially, all positions inside \(S\) will be set to zero.
• Consider tuples of the form \((A[i], i)\) for all \(0 \leq i < N\). Create all these tuples and sort them by their first element.
• Take each tuple \((A[i], i)\) in order, and perform the following calculation: \(S[i] = 1 + \sum_{j=0}^{i - 1}{S[j]}\)

With this, we have successfully calculated the number of ISS that end on each position of the array. The final answer is simply the sum of all elements from \(S\).

You might be thinking, all of this is very nice except for one small detail: the array \(A\) can be very large (its size can be up to \(10^5\)), and calculating all those sums make up for a complexity of \(O(N^2)\), which is prohibitively high!

That’s where our new data structure comes out to save the day. A binary indexed tree —also called a Fenwick tree— is a data structure that can store and update cumulative sums (prefix sums) in logarithmic time, as opposed to the traditional \(O(n)\) from a naive loop to accomplish the same task in an array. The way BITs work is fascinating, in case you want to delve into it a little more, but what’s important in the context of this problem is that by using a BIT, we can calculate all those sums in our algorithm very efficiently. So our problems disappear if we simply choose to implement \(S\) as a BIT (some adjustments are necessary, though, because BITs are not zero–indexed).

There is only one additional detail we haven’t considered yet. What happens if there are repeated numbers in \(A\)? Try it with pen and paper. Create a small array with some numbers occurring more than once. Now try to apply the algorithm described here. Can you identify the exact adjustment that needs to be done? Here’s a hint: it’s related to the sorting of the tuples. They need to be sorted by their first element first, but if there’s more than one tuple with the same first element, then the comparison needs to be done by their second element. But how? I’ll leave it as an exercise… Have fun :).

Ahoy, Pirates!

Problem Name: Ahoy, Pirates!
UVa ID: 11402
Keywords: segment tree, lazy propagation

Working on algorithm problems has been one of my favourite hobbies for a while now, and I’m constantly inspired by the fact that, although there is a finite (and not too large) set of concepts that cover the landscape of all possible problems you can encounter, in practise it feels like there are no boundaries to the amount of things you can learn. In a very real sense, you can always keep learning new things, and the more you learn, the more you find new things that you want to learn next.

I still have many gaps in some basic areas, so I like diving into new things whenever I have the chance to do it. For example, it’s only recently that I have learned a little about a few data structures that were a mystery to me for a long time; segment trees, binary indexed trees, sparse tables, k-d trees… For this reason, I think the next few entries I’ll write for this blog will be for problems related to these data structures. I’ll start with the segment tree by having a crack at this problem —Ahoy, Pirates!— which I think is a very nice exercise for developing a deeper understanding of a ST and the subtleties of implementing update operations on it.

The Problem

Consider a large array of boolean values, represented as zeroes and ones. You have to implement four types of operations that can be performed over this array:

1. Set, or “turn on” a range of adjacent positions in the array (set them to 1).
2. Clear, or “turn off” a range (set to 0).
3. Flip a range (turn zeroes into ones and vice–versa).
4. Query the number of ones in a given range.

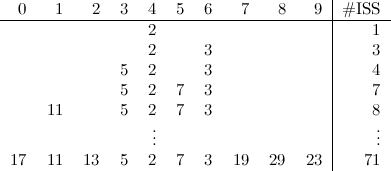
Very interesting problem, if you ask me. We’ll begin with a simple example, as usual. Let’s say we start with an array \(A\) of size 8, and with the following contents:

Querying, First Approach

Now, let’s say we receive a query that asks for the number of ones in a range \([i:j]\) with \(0 \leq i \leq j < N\), where \(N\) is the size of the array (8 in this example). One simple idea is to simply traverse the array with a loop from \(i\) to \(j\), counting the number of ones in the way.

That would be an acceptable solution if that were the only query to answer, or if the number of queries were very low. However, given that the array is big, and there’s a relatively large number of queries, a complexity of \(O(NQ)\) is too high for our needs.

What we’ll do instead is use a segment tree. This is a very nice data structure where a binary tree (typically a binary heap) is built on top of an array in order to store useful information from the underlying data in groups of increasing size. The leaves of the tree correspond to the individual positions inside the array, while internal nodes represent data that is the result of combining information from its children. The root corresponds to an interval that encloses the whole array.

Let’s try to visualise this with our example:

This graph depicts three things for each node in the tree: its interval (enclosed in a purple box), its index (in red) and its contents (in blue), which in this example corresponds to the number of ones in the corresponding interval. Note the convenient way in which the indices of all nodes are related to each other, as is common in heap–like data structures. In this case, the convention is that for a node \(i\), its two children have indices \(2i\) and \(2i + 1\). As you can see, although this data structure represents a tree, it can be stored in a plain array of size 16 (index zero is left unused).

Now, consider why building something like this is useful. If we receive a query that asks for the number of ones in the whole array, we don’t need to go any further than the root of the tree; in other words, an operation that would have taken us \(N\) steps with a common loop, takes us only a single step now. Similarly, if we’re asked about the range \([0:3]\), we just need to visit two nodes: the root and its left child.

Some queries may involve combining the answer from different paths. For example, if we have a query for the range \([2:6]\) then the following nodes of the tree would have to be visited: 1, 2, 5, 3, 6, 7 and 14. This might seem like a bad trade–off in this small example, but it is a huge gain in general. In fact, it’s easy to see that the complexity for an arbitrary query goes from \(O(N)\) to \(O(\log{N})\).

Updating the Tree

So far so good, but what would happen if we try to update the tree after it has been built? Let’s focus on just the Set operation for now.

For the reasons we have discussed before, we should avoid updating the underlying array and then re–building the whole tree; that would have an excessively high complexity. Instead, we can observe this: since every node is implicitly associated with an interval of the array, it’s easy to find out how many positions it covers, and that way we can easily determine the new contents of each affected node after a Set operation.

Back to our example. Let’s say that we receive a query that asks us to set the range \([1:7]\). This is how it could look like just after the relevant nodes have been updated:

The update process (as any operation performed on a ST) starts with the root. The tree is traversed downwards via recursive calls until a node that is completely contained in the relevant interval is found. Those nodes are then updated first (the nodes with blue background). The changes then propagate upwards, as the recursion stops and the stack is popped back until we’re back at the root again (these changes happen in the nodes with gray background).

In this example we can see how, for example, the path from the root to node 9 seems fine and needs no adjustments. Same thing with the sub-tree at node 5, but only by chance, because the contents of that node didn’t change (the range \([2:3]\) of the array already had two ones). However, notice the resulting situation for node 3. At this point, if we received a query asking for the number of ones in an interval that completely contained the range \([4:7]\), we’d have no trouble to find the answer; the information of the root and node 3 is correct. However, the sub–tree at node 3 is inconsistent. If, for instance, we received a query for the interval \([4:5]\), we’d reach node 6 and find the old value of 1 there, which is not correct.

Lazy Propagation

It has been said —by notoriously bright people— that laziness is one of the three great virtues of programmers. As it turns out, laziness is also a desirable property for algorithms. When we update the tree, we don’t want to always propagate the changes down to the leaves (which would be even worse than just updating the original array of integers in a loop). However, we don’t want to leave the tree in an inconsistent state either.

The solution is to extend the tree with an extra field that indicates whether the relevant sub–tree needs to be updated or not. This way, nodes in the tree are properly updated as needed by future queries, and not a moment before; hence the lazy name.

We will extend our tree, then. Since we have three types of operations that change the tree, we’ll store a flag that stores one of four possible values: S for a set operation, C for a clear operation, F for a flip operation, and N for nothing, meaning that the current node is up–to–date —unless one of its ancestors is not N, but that would be handled in due time. This is how our example would look like after the update, with the extended information (there’s a new state field in green):

This tree, unlike the previous one, has now enough information to maintain a consistent state at all times. Note that now nodes 10, 11, 6 and 7 are marked with S, meaning that the next time they are visited, a Set operation will be propagated (lazily) from them. We could have left nodes 10 and 11 untouched because, as has been mentioned, node 5 didn’t change, but we’ll leave them marked just to illustrate the basic process without special checks.

At this point, let’s say that we received a query asking for the number of ones in the range \([4:5]\). This time node 6 is visited, but since it’s marked S, then first we’d have to propagate the Set operation, which means updating the contents of node 6 itself, and then marking its children so the lazy propagation continues with them if necessary. This continuous propagation of previously marked nodes ensures that the information of the tree is always correct, without updating more nodes than necessary. A very powerful technique.

In order to illustrate the operations we haven’t considered yet, let’s say that we also receive a query to Clear range \([7:7]\), and a query to Flip range \([0:3]\). This is how the tree would look like after all these operations:

Okay, to summarise, this is what we’ve imagined so far in our example:

• Building the tree.
• A Query for range \([0:7]\). The result is 4 and is obtained just by looking at the root.
• Queries for ranges \([0:3]\) and \([2:6]\). They need to visit more nodes of the tree, but the result is still obtained in \(O(\log{N})\).
• A Set operation for the range \([1:7]\). It updates directly nodes 9, 5 and 3, and their ancestors, and marks their children so they are lazily updated in the future.
• A Query for range \([4:5]\). This updates node 6 (because it was marked S), and marks its children for future propagation.
• A Clear operation for range \([7:7]\).
• A Flip operation for range \([0:3]\).

The “array” (which lives now inside our ST) now has a total of four ones, yet this is not clear from looking at the leaves alone. You need to analyse the internal nodes to understand how is it that this array has been modified, and what updates have not been propagated yet.

But wait a minute, did you notice how node 14 has a one now, and its state is N? When did that happen? Then answer is, it happened in the middle of the Clear for \([7:7]\). The sequence of events was like this:

1. A Clear for \([7:7]\) was requested.
2. The tree is traversed from the root, and it goes recursively down to nodes 3 and 7. At this point it finds that node 7 is marked S.
3. It propagates this change, which means changing the contents of node 7 to 2, and marking its children (nodes 14 and 15) with S.
4. Immediately after that, it continues with its original request, but to handle it, it has to visit 7’s children first, so it goes down to nodes 14 and 15.
5. This is when the changes happen. I had not mentioned this before, but the way the tree is traversed, it needs to keep visiting nodes, until either a node is completely inside the relevant interval (like node 15 here), or it’s completely outside the interval (like node 14 here). So, node 14 is visited, and since it’s marked S, it changes its value to 1, resets its state to N and it stops traversing this branch.
6. Node 15 is updated according to the Clear request, and stops there as well.
7. All these changes propagate back upwards, resulting in the tree you see in the last figure.

I hope this overview has helped you in case you haven’t worked with segment trees before.

I want to end this by mentioning a curious detail that applies to this specific problem as a result of the operations it involves. Consider the situation of nodes 5, 10 and 11 in the last figure. Node 5 is marked F and its children are marked S. Now consider what would need to happen if, for example, you receive a query for range \([2:3]\). In other words, think about what happens if a node \(u\) with state \(s(u)\) is visited, and one of \(u\)’s children is node \(v\) with state \(s(v)\). How should state \(s(u)\) be propagated down to \(s(v)\)?

There’s a few alternatives:

• If \(s(u)\) is N, then nothing needs to happen.
• If \(s(u)\) is S or C, those operations are overriding, meaning that the state of \(v\) must be set to \(s(u)\) regardless of the previous contents of \(s(v)\).
• However, if \(s(u)\) is F, then the previous contents of \(s(v)\) are important, and they need to change accordingly:
  • If \(s(v)\) was N, it becomes F.
  • C becomes S.
  • S becomes C.
  • F becomes N.

Kinda cool, isn’t it?

Sample Code

I usually don’t include source code in my posts because I prefer describing the general algorithms, but in this case I’ll attach the basics of my segment tree code for this problem, because I know that finding reference code for this data structure on the web can be a little difficult.

This code con be simplified much further by combining similar code from different methods, but this way you can see how every individual operation is implemented separately, and it also makes it easy to identify the common patterns of manipulating the segment tree.

#define MAXN 1024000
#define MAXH 21  // 1 + ceil(log2(MAXN))

// Flags to identify states. 0 is for "Nothing".
#define UP_SET 1
#define UP_CLR 2
#define UP_FLP 3

struct SegTree {
    vector<int> A;  // original array of integers
    vector<int> T;  // segment tree
    vector<int> U;  // segment tree for lazy propagation (the states)

    int n;  // size of the array

    SegTree(int N=0) : n(N) {
        A.resize(MAXN);
        T.resize(1 << MAXH);
        U.resize(1 << MAXH);
    }

    void init() { tree_init(1, 0, n-1); }
    void tree_init(int x, int a, int b) {
        U[x] = 0;
        if (a == b) { T[x] = A[a]; return; }
        int lt = 2*x, rt = lt + 1, md = (a+b)/2;
        tree_init(lt, a, md);
        tree_init(rt, md + 1, b);
        T[x] = T[lt] + T[rt];
    }

    void set(int i, int j) { tree_set(i, j, 1, 0, n - 1); }
    void tree_set(int i, int j, int x, int a, int b) {
        propagate(x, a, b);
        if (j < a || i > b) return;
        if (a == b) { T[x] = 1; return; }
        int lt = 2*x, rt = lt + 1, md = (a+b)/2;
        if (a >= i && b <= j) {
            T[x] = b - a + 1;
            U[lt] = U[rt] = UP_SET;
            return;
        }
        tree_set(i, j, lt, a, md);
        tree_set(i, j, rt, md + 1, b);
        T[x] = T[lt] + T[rt];
    }

    void clear(int i, int j) { tree_clear(i, j, 1, 0, n - 1); }
    void tree_clear(int i, int j, int x, int a, int b) {
        propagate(x, a, b);
        if (j < a || i > b) return;
        if (a == b) { T[x] = 0; U[x] = 0; return; }
        int lt = 2*x, rt = lt + 1, md = (a+b)/2;
        if (a >= i && b <= j) {
            T[x] = 0;
            U[lt] = U[rt] = UP_CLR;
            return;
        }
        tree_clear(i, j, lt, a, md);
        tree_clear(i, j, rt, md + 1, b);
        T[x] = T[lt] + T[rt];
    }

    void flip(int i, int j) { tree_flip(i, j, 1, 0, n - 1); }
    void tree_flip(int i, int j, int x, int a, int b) {
        propagate(x, a, b);
        if (j < a || i > b) return;
        if (a == b) {
            T[x] = T[x] == 1 ? 0 : 1;
            return;
        }
        int lt = 2*x, rt = lt + 1, md = (a+b)/2;
        if (a >= i && b <= j) {
            T[x] = (b - a + 1) - T[x];
            U[lt] = apply_flip(U[lt]);
            U[rt] = apply_flip(U[rt]);
            return;
        }
        tree_flip(i, j, lt, a, md);
        tree_flip(i, j, rt, md + 1, b);
        T[x] = T[lt] + T[rt];
    }

    int query(int i, int j) { return tree_query(i, j, 1, 0, n-1); }
    int tree_query(int i, int j, int x, int a, int b) {
        if (j < a || i > b) return -1;
        propagate(x, a, b);
        if (a >= i && b <= j) return T[x];
        int lt = 2*x, rt = lt + 1, md = (a+b)/2;
        int q1 = tree_query(i, j, lt, a, md);
        int q2 = tree_query(i, j, rt, md + 1, b);
        if (q1 < 0) return q2;
        if (q2 < 0) return q1;
        return q1 + q2;
    }

    int apply_flip(int v) {
        if (v == UP_SET) return UP_CLR;
        if (v == UP_CLR) return UP_SET;
        if (v == UP_FLP) return 0;
        return UP_FLP;
    }
    void propagate(int x, int a, int b) {
        if (U[x] == 0) return;
        if (U[x] == UP_SET)
            T[x] = b - a + 1;
        else if (U[x] == UP_CLR)
            T[x] = 0;
        else if (U[x] == UP_FLP)
            T[x] = (b - a + 1) - T[x];

        if (a != b) {
            int lt = 2*x, rt = lt + 1;
            if (U[x] == UP_SET || U[x] == UP_CLR)
                U[lt] = U[rt] = U[x];
            else
                U[lt] = apply_flip(U[lt]), U[rt] = apply_flip(U[rt]);
        }
        U[x] = 0;
    }
};

Highest Paid Toll

Problem Name: Highest Paid Toll
UVa ID: 12047
LightOJ ID: 1379 (under the name “Toll Management”)
Keywords: graph theory, single source shortest path, dijkstra

Let me share with you a little story from my childhood. When I was a kid, one of the first books I really enjoyed —and one which remains a cherished piece in my bookshelf to this day— was a mathematics book they made me read in elementary school. It wasn’t your average elementary math book, however. It was written by a professor from a local University, and the book had a very friendly and humorous approach to the concepts it presented (without being patronising), and at the same time it was rich in content and rigorous. It also contained a good deal of material not directly related to mathematics, like philosophy, literature, humanities, puzzles… well, you get the idea. In short, to a small curious kid with a yearning for understanding more about this world, this book was (and still is) simply fantastic. Anyway, one of the lessons I learned from it comes at the beginning of the section devoted to puzzles, where some general ideas for problem–solving are discussed. That chapter contains a list of tips to approach a new problem, and among them is the question “Can you make a drawing?”, and then in a smaller font (the “informal” voice inside the book) there was the complementary statement: “you can always make a drawing, do it!”

The point of this long–winded introduction is simply this: you can indeed always do a drawing… give it a try. This is not a novel idea by any means, of course, it’s just one that was strongly impressed upon my memory from those days, and which I apply constantly ever since. Granted, most of the time I try to do the “drawing” in my mind, whenever I’m able to fit the entire problem in my head, but if I can’t do that I quickly resort to a pen and a sheet of paper and start doodling around. This problem is just an exceptionally good example of an instance where something that was initially confusing, all of a sudden revealed its simplicity and elegance once I just started drawing things. This will all become clear in a moment —at least I hope so, if not, try doing a drawing about this post, a meta–drawing if you will :).

Here’s the summary of the problem. You receive a directed, weighted graph. Two nodes are defined as source (\(s\)) and sink (\(t\)), and you also receive a number \(p\) which denotes a “cost limit”. You have to find the heaviest edge inside any valid path between the source and the sink; a path is valid if its total cost doesn’t exceed \(p\).

Clearly, this is not your standard single–source shortest path problem. However, there is a nice solution based on the SSSP algorithm. As usual, let’s begin with an arbitrary example that helps us tame this puzzle. Consider the following graph:

Try to find the answer for this example. That is, identify all paths from 1 to 9 with a total cost less than or equal to 100, and among those paths, determine the edge with the largest cost. Given that the answer becomes obvious from the following graphs, I might as well tell you now that it is the edge \(2 \rightarrow 4\) with a cost of 53.

What I will ask you now is, forget about this specific example. Generalise things in your mind. The next graph presented below will look familiar, but keep in mind that this is just a simplified representation of the general problem. You can be fairly certain that the real test cases for this problem from the judge will contain all kinds of complicated graphs, with many more nodes, edges, multiple edges between the same pair of nodes, unconnected components, etc. But this representation is just an aid that helps us wrap our minds around the core of this problem.

That being said, imagine now an arbitrary graph for which there is a valid answer. That means that there is one edge that belongs to a valid path from the source to the sink, and that edge has the highest cost possible among all the alternatives. Let’s paint that edge with a distinctive color, like red. That graph might look something like this:

Okay, now… if this edge, let’s call it \(u \rightarrow v\), really exists and is a valid answer, then it implies a number of things:

• There has to be a path \(s \Rightarrow u\).
• Similarly, there exists a path \(v \Rightarrow t\).
• Perhaps the most significant implication of all, the sum of the costs of \(s \Rightarrow u\), \(u \rightarrow v\) and \(v \Rightarrow t\) has to be less than or equal to \(p\).

Let’s put all this information in a new graph that depicts the relevant nodes and paths:

When you think about the green paths, does anything come to mind? For me this was the moment when something “clicked” in my head. I started having no idea how to solve the problem, but when I drew something like this the strategy made itself evident; but let’s keep going.

I hope you can see where this is going. If there is an edge \(u \rightarrow v\) that is our answer, then it would be useful to know the shortest possible paths \(s \Rightarrow u\) and \(v \Rightarrow t\), wouldn’t you agree?

With this in mind, let’s formulate the following algorithm to solve the general problem:

• Start with two graphs: the original graph (let’s call it \(G\)) and a reverse graph (let’s call it \(R\)).
• Find all shortest paths in \(G\) from \(s\).
• Find all shortest paths in \(R\) from \(t\).
• Let \(A\) be the answer. Initially, \(A = -1\).
• For each edge \(u \rightarrow v\) in \(G\) with cost \(w\):
  • Determine the total cost \(C\) of \(w\) plus the shortest paths \(s \Rightarrow u\) in \(G\) and \(t \Rightarrow v\) in \(R\).
  • If \(C \leq p\) and \(w > A\), then set \(A = w\).

That’s it. Running an algorithm like Dijkstra’s two times and then traversing over all the edges is quite enough to reach the solution.

Needless to say, the best part for me was having an Eureka moment right after doing one of my primitive drawings in a piece of paper. This is what intrigues me, though: the drawing I did was not particularly “interesting”; it was just a rather generic graph. Yet somehow, seeing the nodes and edges drawn in a piece of paper, and assigning colors to some edges made all the difference. It’s like it made all the processes inside my brain go faster… Maybe you understand what I’m talking about. If you don’t, can I suggest that you try doing more drawings in the future? Even if they are so trivial that it might seem silly to spend the time drawing something so elementary. The results might surprise you.

Jogging Trails

Problem Name: Jogging Trails
UVa ID: 10296
LightOJ ID: 1086
Keywords: graph, dynamic programming, eulerian cycle, floyd-warshall, bitmask calculations, chinese postman

In the world of competitive programming, it is very common to come across problems that place the focus on just one or two main algorithmic concepts, such that you can more or less solve them by simply following a “standard” recipe, or by doing a few simple variations over the classic algorithms. However, not every problem is like that.

There are problems that involve several different concepts, and their algorithmic elements intertwine in interesting and elegant ways to create a new type of challenge. A challenge that provides great satisfaction and a powerful sense of fulfillment once you find out a valid way to rearrange and mix the ingredients from different recipes to create your own solution. Moreover, from my own limited experience observing the work of some of the greatest competitive programmers on the planet, it is my belief that perhaps the main difference between them (the really, really good algorithm problem solvers), and the average programmers —beyond the obvious things, like the amount of experience and knowledge—, is their deep understanding of the “recipes” and their creativity to mix them in order to solve a new complex problem.

Jogging Trails, the problem I’ll talk about here, is a relatively “simple” problem, but it’s a very nice example of this type of beautiful “intertwining” of different concepts. It’s easy to summarise the problem like this: you receive a weighted, undirected and connected graph; you have to find the “cost” of the shortest route that starts and ends on the same vertex after visiting every edge at least once. This is also known as the Chinese postman problem, or the route inspection problem.

There are many interesting things to talk about in this problem, so we’ll approach them gradually. Let’s start with an example to help us illustrate our ideas down the road. Consider the following graph:

Okay, first things first. Try to manually find the solution for this example. Finding it quickly is not very easy. One of the first things you’ll probably notice is that it’s tricky to find a route that starts and ends on the same node, after having visited each edge exactly once. In fact, it’s impossible.

This is where the first interesting algorithmic idea comes to play, and it is that of an Eulerian cycle or circuit. It simply refers to a cycle inside a graph that visits each edge exactly once. What is useful to remember is this (quoting from Wikipedia):

An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component.

In other words, assuming you have a connected graph (like in our case), count the number of edges connected to each node and if every node has an even number of them, then you absolutely can do a tour that starts and ends on the same place, and visits all edges exactly once. This means that if our example showed that property (every node had an even degree), then we would not have to do anything special, the answer would just be the sum of weights of all edges. Simple, right? Remember that we don’t need to calculate the path itself, just its cost.

However, we aren’t that lucky in our example. We have five nodes, and four of them have an odd degree. What this implies is that whatever shortest path there might exist in there, it must visit some edges more than once, there’s no other way around it. The question is, obviously, which edges will we have to visit twice or more? Actually, we don’t really need to know which edges, just how much additional cost will they represent for our final answer.

At this point, it could be useful to apply a general strategy that is usually seen in graph–related problems. If you know of a certain algorithm or idea that can help you but it can’t be applied to your graph directly, try modifying your graph until it does! This is a common technique used, for example, when you want to calculate things like the max flow in a network and so you invent “dummy” nodes and edges in order to apply the algorithm properly.

In this case, what if we think about “dummy” edges that can turn all nodes into even–degree nodes? Something like this:

There are many possible ways in which these fake edges could be created to make this graph favourable for finding an Eulerian cycle. We could, for example, connect nodes \((2, 3)\) and \((1, 4)\), or we could do \((2, 1)\) and \((3, 4)\), and for each of these connections there are many ways to do it as well. For instance, for the fake edge \((2, 3)\) there are many ways to go from 2 to 3, like going directly (with a cost of 25), or going through node 1 (with a cost of 23). It is important to keep in mind that the fake edges are just something to help us model the graph as something where you can actually find an Eulerian tour, but they just represent paths that exist over the real edges.

In any case, what we’re interested in is a combination of fake edges that provide the minimal additional cost. So we arrive to the second algorithmic idea to be applied in this problem. In order to try the different available combinations that can form our fake edges, it is in our best interest to find out the shortest paths between all pairs of nodes, and since the number of nodes in the graph is very low (\(n \leq 15\)), the Floyd-Warshall algorithm fits the bill perfectly.

After this step, we would end up with the following information:

A little examination should reveal that the best possible combination of fake edges among the nodes \((1, 2, 3, 4)\) would be from the shortest paths between \((1, 2)\) and \((3, 4)\). Our extended graph would then look like this:

Try finding the solution now. Doing an Eulerian tour is now a breeze, and it is pretty evident that the edges that have to be visited twice are \((2, 1)\), \((4, 5)\) and \((3, 5)\). The final answer for this example is 109, the sum of all edges in this extended graph.

We are getting close, but we still haven’t figured out just exactly how are we going to find the best combination of fake edges. This is where the third and final algorithmic concept comes in: dynamic programming, with a little bit of bitwise manipulations.

Again, because the number of nodes is small, it is feasible to formulate the following D.P. relation:

\(f(S)\)

The minimum cost of connecting pairs of nodes among the set \(S\) (represented as a bitmask in code).

This relation is very simple: the base case is an empty set of nodes, which has a cost of zero; otherwise we try every pair \(P\) of nodes among the set, and find the sum of the shortest path between the pair of nodes and the value of \(f(S - P)\). We keep the overall minimum of these values.

Let’s see an example of a top–down implementation of this in C++:

#define MAXN 15
#define INF  (1 << 30)

#define GetFS(b) ((b) & -(b))       // get first set bit
#define ClrFS(b) (b &= ~GetFS(b))   // clear first set bit

static const int m37pos[] = {
    32,  0,  1, 26,  2, 23, 27,  0,  3,
    16, 24, 30, 28, 11,  0, 13,  4,  7,
    17,  0, 25, 22, 31, 15, 29, 10, 12,
     6,  0, 21, 14,  9,  5, 20,  8, 19, 18
};
#define Ctz(x) (m37pos[(x) % 37])   // count of trailing zeroes


typedef unsigned int u32;


// We assume that this matrix contains the shortest paths among all pairs of
// vertices (i.e. after running Floyd-Warshall)
int g[MAXN][MAXN];

// Memoization structure
int memo[1 << MAXN];


/**
 * Minimum cost of increasing by one the degree of the set of vertices given,
 * to make them even.
 *
 * @param b Bitmask that represents the nodes with an odd degree
 * @return The minimum cost
 */
int f(u32 b)
{
    if (b == 0) return 0;
    if (memo[b] >= 0) return memo[b];

    int best = INF;

    int nv = 0;    // number of vertices in the bitmask
    int vs[MAXN];  // list of vertices

    // populate list of vertices from the bitmask
    for (u32 r = b; r; ClrFS(r)) {
        u32 x = GetFS(r);
        vs[nv++] = Ctz(x);
    }

    // try all pairs of vertices
    for (int i = 0; i < nv; ++i)
        for (int j = i + 1; j < nv; ++j) {

            u32 p = (1 << vs[i]) | (1 << vs[j]);
            int cur = g[ vs[i] ][ vs[j] ] + f(b & ~p);

            if (cur < best) best = cur;

        }

    return memo[b] = best;
}

There are a few interesting things in here for you to analyse if you haven’t done this kind of “bitwise” D.P. before, but they are very accessible once you are familiar with bitwise manipulations. The code from lines 4–13 just provides a few useful macros to deal with bits —the code for Ctz comes from Bit Twiddling Hacks, a very useful resource for you to explore, if you haven’t done so already.

There are two external data structures (lines 21 and 24) that we depend on, and then the D.P. function itself is defined on line 34. In order to call this function you need to fill the memo array with the value -1, and then pass the bitmask of all vertices with odd degree as a parameter. The value returned by f plus the sum of all edges in the original graph provide the final answer.

And now we have reached the end. We took elements from different algorithmic areas (graph theory, cycles, shortest paths, dynamic programming, bitwise calculations) to solve the Chinese postman problem. Wasn’t it fun?

The Vindictive Coach

Problem Name: The Vindictive Coach
UVa ID: 702
LightOJ ID: 1173
Keywords: counting, dynamic programming

Isn’t it interesting how everything changes constantly, including ourselves, even without us noticing? I mention this because I was a little amused by the fact that I recently came back to this problem, which I tried to solve some time ago (unsuccessfully at the time, of course), but now the solution just popped in my mind almost immediately in a natural way. This is just very intriguing to me; how our minds work, and how things that some people may consider “difficult” seems genuinely “easy” to others and vice–versa, and how our conscious (and unconscious) learning modify these perceptions with time.

Anyway, let’s get back to this problem. It asks us to consider sequences formed by the first \(N\) positive integers, such that, starting with an arbitrary \(m\) (\(1 \leq m \leq N\)), it alternates between smaller and bigger numbers until all \(N\) integers have been used exactly once. The first number in the sequence has to be \(m\), then a smaller number must come next, then a bigger number, then smaller, and so on. For example, with \(N=5\) and \(m=3\) a valid sequence could be \(S_1=(3, 2, 5, 1, 4)\) but \(S_2=(3, 1, 4, 5, 2)\) and \(S_3=(3, 4, 1, 5, 2)\) would be invalid. In \(S_2\), after 4 there should be a smaller number, and in \(S_3\), the alternating sequence has to start by going “down”, so 4 can’t go second.

There is one special case that was a little confusing to me at first because of the wording from the problem statement. It happens when \(m=1\) (and only then). In that case, since it isn’t possible to start the sequence by going “down” to a smaller number, then it starts going up, but to the closest possible number that allows the zig-zag nature of the sequence to be maintained. In other words, if \(m=1\) and \(N>2\) then the second number of the sequence has to be 3, and then the sequence continues normally: \((1, 3, 2, \dots)\).

The question is simply, given the values of \(N\) and \(m\), how many valid sequences can be formed with the rules described? Now, it should be clear that at its core, this is a counting problem, where dynamic programming just happens to be a valid strategy to compute the answer easily. The trick is in formulating a relation that leads us to the answer.

Let’s generalise things a bit, and say that we have a list of \(k\) positive integers in ascending order, and we have just selected the \(i\)th element (\(1 \leq i \leq k\)) to be placed in the sequence. Now, the list has been split in two: there would be \(k - i\) elements left “above” our last selection (let’s call that group \(A\)), and \(i - 1\) elements “below” (we’ll call it \(B\)). Depending on the direction of our last movement (“up” or “down”), the next number would have to be selected from one of the two groups, \(A\) or \(B\). Let’s call \(a\) the number of elements in \(A\) and \(b\) the number of elements in \(B\). Let’s call \(n\) the last number added to the sequence so far.

To illustrate this a little bit better, let’s go back to the example \(N=5, m=3\). After picking the first number of the sequence, things would look like this:

\(A=(4, 5) \;;\; B=(1, 2) \;;\; a=2 \;;\; b=2 \;;\; n=3\)

We can now formulate the following:

\(f(a, b)\)

The number of sequences that can be formed from \(a\) numbers bigger than \(n\) and \(b\) numbers smaller than \(n\), where the next number has to be chosen from \(A\).

This takes care of our “up” movements, but we also need to handle the “down” case, so here’s the symmetrical \(g\):

\(g(a, b)\)

Similar to \(f\), but the next number has to be chosen from \(B\).

The base case would be when the number of elements to choose from is either zero or one:

Then the main D.P. relation would look something like this:

Let’s see how it works; let’s consider the \(f\) relation that describes the “up” movements —the reasoning for \(g\) is very similar. We have to select one number from the \(A\) group. We have \(a\) different choices for this next movement, and this is represented by \(f(a, b)\). If we choose the smallest number in that group, then we leave two groups: a new \(A\) with \(a'=a-1\) elements and \(B\) remains the same. If we choose instead the second smallest number, then the groups change in size as follows: \(a'=a-2\) and \(b'=b+1\) (because by choosing the second smallest number, the very smallest number moves into the \(B\) group). The same thing applies for the third smallest number, the fourth, and so on, and that’s what the summations represent.

Going back to our example \(N=5, m=3\), we know we have two options for the second number of the sequence: we can pick 1 or 2. If we picked 1, the new situation would be:

\(A=(2, 4, 5) \;;\; B=() \;;\; a=3 \;;\; b=0 \;;\; n=1\)

If we picked 2 instead, it would be:

\(A=(4, 5) \;;\; B=(1) \;;\; a=2 \;;\; b=1 \;;\; n=2\)

All of this information is for illustration purposes, but you can notice that the actual contents of \(A\) and \(B\), as well as the last number picked \(n\) are irrelevant. The only thing that matters in our algorithm is the values \(a\) and \(b\) and whether the next movement has to be “up” or “down”.

Notice also that this process is guaranteed to end at some point because the total number of elements used as arguments for \(f\) and \(g\) are being decreased by one at each step. This leaves us with an algorithm that can compute all possible answers in \(O(N^3)\). This is a pre–calculation that happens only once in the program, and then each test case can be answered in \(O(1)\). If \(m > 1\) then the answer would be \(g(N-m, m -1)\). The small adjustment for the case \(m=1\) is left as an exercise for the reader :).

Tiles

Problem Name: Tiles
LightOJ ID: 1244
Keywords: recursion, matrix exponentiation

This is a problem involving an interesting recurrence that combines different inter–dependent relations. Moreover, given the large range of the input, it can be tackled with matrix exponentiation instead of classic dynamic programming.

You have a rectangular board of size \(2 \times N\) that is to be filled with tiles of six different types. 2 tiles are formed by two squares (each of size \(1 \times 1\)) and have the shape of a bar. The remaining 4 tiles have three squares, representing the four different rotations of a L–shaped tile. The tiles have to be placed in the board as–is (without rotating or flipping them).

We’ll identify the six tiles by the characters \(A, B, \dots, F\). This is how they look, using a single lowercase character to represent each square:

a      c   dd   e  ff
a  bb  cc  d   ee   f

The question is, in how many different ways can the board be filled using the six tiles?

It shouldn’t take long to see that it would be convenient to start by defining the following function:

\(f(n)\)

Number of ways to completely fill a board of size \(2 \times n\).

However, there is not a straightforward solution from just this relation —at least not one that I can see. Something that helps here is looking at a couple of additional “states” that can be analysed and used to build our final answer.

Consider the following auxiliary functions:

\(g(n)\)

Number of ways to fill a board of size \(2 \times (n-1)\), leaving a single square in the top row of the \(n\)th column.

and finally,

\(h(n)\)

Number of ways to fill a board of size \(2 \times (n-1)\), leaving a single square in the bottom row of the \(n\)th column.

Think for example of what happens when you have completely filled a section of the board of size \(2 \times k\), going from left to right, and you append a \(C\) tile. Then you have filled an area of \(2 \times (k+1)\), but you have an additional single square at the bottom of column \(k+2\). Those are the situations where \(g\) and \(h\) will prove useful.

Also, having these three relations make it possible to now formulate a definition of \(f(n)\):

These expressions come directly from thinking about the different ways to place the six tiles inside the board. Let’s take \(f(n)\) for example. By definition, \(f\) concerns itself only with filling the first \(n\) columns entirely, so it shouldn’t include cases where the tile \(C\) and \(D\) are placed last. It only considers the cases where the last tile is either: \(A\), represented by the term \(f(n-1)\); or \(B\), which leads to \(f(n-2)\) (using two \(B\) tiles one on top of the other); or \(E\) and \(F\), which lead to \(g(n-1)\) and \(h(n-1)\) respectively.

The definitions of \(g(n)\) and \(h(n)\) come from a similar reasoning. Try to deduce them by yourself thinking about the different ways in which you can leave one single square in the last column. The beauty of this is that now all the terms show recurrence and lend themselves to a matrix exponentiation strategy quite nicely.

Let’s outline two of the three matrices, leaving the matrix with the coefficients for last:

Now here’s the crucial step for our implementation. Given our previous definitions of \(f\), \(g\) and \(h\), we fill the matrix \(A\):

With this now we can write the implementation, and obtain the answer in \(O(k^3 log N)\), with \(k=4\).

Aladdin and the Magical Sticks

Problem Name: Aladdin and the Magical Sticks
LightOJ ID: 1342
Keywords: math, probability, expected value, memoization, harmonic number

I’ve always had a keen interest in problems related to numbers, counting, probability and so on. It is only recently, however, that I’ve started to grow aware of the reasons why this might be so. Let’s take this problem as an example. After I read its description for the first time, I knew I would not rest until I found a satisfactory solution, and going into it I recognised that right then I still had some gaps in my knowledge, but still, it was thrilling to know that I was about to tackle something that would lead me to learn new things. It is a little hard to put into words, but there’s just something deeply enjoyable when you encounter a problem that you know you can’t yet solve, but your intuition tells you that you’re close; in other words, even if it’s a little beyond your current knowledge or skill, it’s within your reach. This is something that I’ve personally experienced with many math–related problems, and that’s probably the main reason why I find them fascinating.

Anyway, back to the subject at hand, this problem tells us the story of Aladdin, who is presented with a group of sticks, each one with a certain weight. He is asked to pick up the sticks, one by one, and every time he picks a stick, it is returned to the group and he has to continue picking sticks until all of them have been chosen. There’s a couple of extra details of importance: initially, the probability of picking any one stick is the same for all sticks, but, there’s also two types of sticks. One type is easily recognisable by Aladdin, so every time he picks a stick of this type, he doesn’t pick that same stick again. The other type of stick is normal and there is no way to recognise it, so sticks of this type could be picked many times. The question is: what is the expected weight of all the sticks Aladdin has to pick until all sticks have been chosen?

You may have noticed that this problem has a similar “flavour” to the Dangerous Maze problems —and they are, after all, from the same problem setter :). We could even rewrite the problem statement and use doors instead of sticks, and distances instead of weights, and the problems would look pretty similar. However, there is one crucial difference; in this problem you don’t “get out” until you have picked all sticks (or doors).

This difference turns this into an entirely different kind of problem. To give you some idea about the nature of the problems I’m talking about, think about how to calculate the expected number of throws of a single die until it shows a certain number, and how it differs from calculating the expected number of times you have to throw a die until you have seen all of its sides. Another way to look at it is to think about sticker albums or collectible card games. Let’s say that you can buy one card at a time, which comes completely at random (all cards with equal probability). How many cards do you need to buy until you complete your collection?

Not surprisingly, this is a classic conundrum known as the Coupon collector’s problem, and the math behind it is actually fairly accessible once you’re familiar with the basics of probability and expected value. Quoting from Wikipedia:

The key to solving the problem is understanding that it takes very little time to collect the first few coupons. On the other hand, it takes a long time to collect the last few coupons.

Let’s go back to the example with dice. Let’s say you want to know the expected amount of tosses until you have seen all sides from a standard die. You can split this problem into six sub–problems: how many tosses until you see the first “new” (previously unseen) side? How many tosses after that until you see the second “new” side? And so on until the sixth and final “new” side.

It’s easy to see that the first sides come up pretty quickly —you are guaranteed to see a new side on your first toss, and it’s very likely that you’ll see a new side on your second toss because the chance of repeating your previous toss is only \(1/6\). It’s the last unseen sides that take longer to come up. This leads to a very elegant formula for the expected value in the coupon collector’s problem. Using the terminology of this problem, if all sticks were of the second type (the type that is unrecognisable), then the expected amount of times that Aladdin would have to choose a stick until all of them were picked would be:

Where \(H_n\) is the \(n\)th harmonic number. At this point, I’d like to say that it’s very possible that you have now enough elements at your disposal to solve this problem. If you haven’t done so already, I suggest you take at least a couple of minutes right now to think about the mathematics of it, and try to formulate a solution —even a preliminary one. Nothing can replace that type of mental exercise.

Okay, now here’s what I found to be the final piece of the puzzle to arrive to my solution; it’s something I call “complementary” or “background–foreground” thinking (there’s probably a better name for it, but this is how I think of it). Edit: After re–reading some passages of one my favourite books ever —GEB— I can see that this concept is usually referred to as “Figure and Ground”. I’ll try to remember this…

Let me give you an example. Maybe you have confronted the Birthday paradox before, where you want to calculate the exact probability that any two people in a group of \(n\) people have the same birthday. You can approach this in two different ways, and one of them is going to be vastly easier than the other. You can try to go “straight” to the solution (what you see in the foreground) and consider every pair of people and the probability that they do have the same birthday. Obtaining the answer through this process is very complicated because of the relations formed between the pairs and the fact that you want to know the probability of any pair having the same birthday. The other approach is looking at the background or complement, and think of the probability that the \(n\) people have all different birthdays (let’s call it \(\bar{p}\)), and then your answer comes from the complement \(1 - \bar{p}(n)\). Much easier to calculate.

I hope the crux of the matter is clear. Sometimes if you can’t solve a problem looking at the foreground, it might be useful to look at the background and try to solve it from there. This is what I applied here. The idea is to initially consider all sticks as if they were of the second type; this gives us an initial expected weight \(W_i\). After that, subtract from \(W_i\) a weight from the sticks of type 1, proportionate to the “excess” in our calculation.

Why an “excess”? Well, it should be easy to see that if some of the sticks are of type 1, then our first estimation \(W_i\) is larger than the right answer, because no matter how we look at it, all sticks of type 1 are picked only once, no more. Let’s call \(\hat{E}\) the expected amount of times that one particular stick would be picked, if all sticks were of type 2. Then we have:

However, for sticks of type 1, this expected value is exceeded by the following amount (\(E_x\)):

Alright, now we can formulate the following algorithm:

• Let \(A_T\) be the average weight of all the sticks.
• Let \(E\) be the expected number of sticks that have to be picked (if all were of type 2). This comes directly from the coupon collector’s problem as \(E=n \cdot H_n\).
• \(W_i = A_T \cdot E\)
• If there is one or more sticks of type 1:
  • Let \(N_1\) be the number of sticks of type 1 and \(A_1\) the average weight of the sticks of type 1.
  • \(W_f = W_i - N_1(H_n - 1) \cdot A_1\)
• Else, \(W_f = W_i\)

Our answer is \(W_f\).

Turn the Lights Off

Problem Name: Turn the Lights Off
UVa ID: 10309
Keywords: brute force

I find this problem interesting for a number of reasons, but the first that comes to mind is that it involves a game with simple rules which anyone can pick up quickly, but its mathematical analysis is not trivial at all —and games of this kind are just fantastic, aren’t they?

Let’s start by mentioning that the solution I implemented can be classified as “brute force”, but if you think that it’s a naive brute–force (\(2^{100}\)), then we’re not on the same page, yet.

Actually, the first thing I did when I first read this problem was thinking about all the types of “blind” strategies and possible pruning that could be performed while looking for the solution through a breadth–first search. The results were not very encouraging. As you may have noticed, the space of possibilities is insanely large (\(2^{100}\)) and a BFS could end up using equally lunatic amounts of memory. The problem boils down to the simple fact that representing a “state” for this problem is not cheap: a boolean matrix of size \(10 \times 10\) is simply too much for any simple–minded approach.

Now, fortunately for us, some pretty smart people have worked hard on analysing this game in the past, and we can read about their findings through the magic of the Web :). First of all, as far as I know, the original game that implemented these mechanics is called Lights Out and was developed by a company called Tiger Toys in 1995, in case you want to do some research by yourself. If you do, one of the first website you’ll probably come across is this: Jaap’s Puzzle Page, which has a lot of information about it. There’s a related page dedicated exclusively to the mathematics behind Lights Out, which are fascinating to read about, but I won’t mention here mainly because my solution didn’t involve any sophisticated math analysis.

What I do want to mention though, is that there exists an heuristic that can be used to solve these puzzles, which can be summarised like this: press some buttons (i.e. switch some lights) from the top row, then “chase the lights” from the second row to the bottom. What this means is, starting with the second row, press a button only if the light to the north of the current position is on. Go on like this row–by–row until you reach the bottom. If in the end you haven’t cleared the grid, then go to the beginning, pressing some buttons from the top row, and repeating the process until you have solved it. Interesting, right?

But it gets better. In a paper —referenced in Jaap’s page— called “Turning Lights Out with Linear Algebra” we can find the following good news:

Lights Out can be generalized to an \(n \times n\) array of lights. (…) Of course if the dimension of the null space is zero, every configuration is winnable and the solution is unique (if no buttons are pressed more than once).

And then there’s a table where we find that the dimension of the null space for games of size \(10 \times 10\) is zero. In other words, for this problem, every configuration has a solution, and if we find it by “pressing a switch” no more than once, then it’s guaranteed to be the best solution.

Now we’re ready to formulate our solution: if we try pressing every combination of lights from the top row and then “chase the lights” downwards, we have to check only \(2^{10}\) alternatives, which are guaranteed to be enough to find our answer. I was truly amazed by how nicely this idea translates into elegant code, and it has a complexity of \(O(2^n n^2)\) (where \(n=10\) for this problem).

By the way, if you have some time to spare, maybe you’d like to give the heuristic explained here a try, on a game of “Lights Out” where the size of the grid increases at each level: here’s the game of Tacoyaki+. Have fun :).

---

References

• Turning Lights Out with Linear Algebra by M. Anderson and T. Feil (1998). Math Magazine, vol. 71, no. 4, October 1998, pp. 300-303. http://www.math.ksu.edu/~dmaldona/math551/lights_out.pdf

Olympic Swimming

Problem Name: Olympic Swimming
UVa ID: 11546
LightOJ ID: 1423
Keywords: sweep line, hashing

The London 2012 Olympics closing ceremonies took place just a couple of days ago, and it has given me a nice excuse to work on a problem that somehow involves an Olympic event :). Actually, I had this problem near the front of my queue of “to do” problems and it coincidentally emerged during these days of “Olympics fever”. The real reason I find it noteworthy, however, is that it also gives me the opportunity to talk about a couple of interesting concepts that I have not talked about in previous posts.

The problem can be summarised as follows: imagine a swimming pool with length L metres (\(L \in \mathbb{Z}\)). This pool has K lanes, and marks at every metre, so you can imagine it as the sum of \(L\) sections, each one 1 metre long and with \(K\) lanes. The pool has a number of hurdles or obstacles (it doesn’t make much sense in real swimming events, but never mind that), such that each hurdle is placed on a particular lane, between two consecutive marks.

The question is, if you can divide the pool only at a mark, what is longest possible segment of the pool in which all the lanes have the same number of hurdles (not necessarily at the same locations)?

Let’s start by looking at an example to help us analyse this problem. Consider a pool of length 10 and with three lanes. The lanes will have 3, 4 and 2 hurdles, as depicted in the following figure:

Try to find two marks \((i, j)\) such that all lanes have the same amount of hurdles in that segment of the pool and \(j - i\) is maximised. After some trial and error, it should become clear that the longest segment is \((5, 9)\), with a length of 4 and one hurdle per lane.

Now we can discuss the first interesting concept that this problem leads us into, which is the sweep line algorithm. The idea behind this is simple (although the specific details for certain problems might not be simple at all): you have a geometric plane and a set of points that relate to your model of a problem; you use an imaginary line that is moved over the plane, and every time it hits one or more points, some type of calculation is performed. In this way you’re computing a certain value gradually with an algorithm that has, at first, a complexity of \(O(n)\) —not counting the operations you perform at each “collision”. This type of algorithm can be applied to many interesting geometry–related problems, like finding the closest pair of points in a set (see problem UVa 10245) or computing the outline of the union of a set of rectangles with a common baseline (see problem UVa 105).

We’ll apply the general principle to this problem, but first let us give it a little more thought and find out how a sweep–line strategy may be useful. One of the first things to notice is that if you start at the mark \(i=0\) and move forward all the way to \(i=L\), the number of hurdles at each lane can only increase or stay the same at each step, so maybe a prefix sum can help us get closer to the answer. Let’s start by defining the following:

\(P_{i}\)

A tuple with the prefix sums of hurdles at position \(i\). Each element in the tuple corresponds to one lane.

According to this definition, the values of \(P\) for our example are:

Do you notice anything particularly interesting in this list, keeping in mind that we know that our answer is in the segment \((5, 9)\)? You should see that the relative differences among the elements in \(P_5\) are the same as in \(P_9\). In fact, those two tuples form the pair that is the most distant while having the same relative differences internally. To see it more clearly, let’s bring a second definition that simplifies things for us:

\(R_i\)

A tuple where each element \(R_{i, j} = \text{max}(P_i) - P_{i, j}\)

Now we have enough elements to formulate our main algorithm. If we use a sweep–line, we could calculate \(R_i\) and \(R_{i+1}\) at each point \(i\) given in the input and every time we find an \(R\) tuple that we have seen before, we calculate the distance between the new mark and the old mark, and our final answer comes from choosing the overall maximum.

This brings us to the second concept that I want to talk about —hashing. You see, a sweep line by itself is just a very basic approach, but what’s important is the type of operations you do at each critical point you find in your sweep, which commonly requires keeping track of data (inserting, querying, deleting) very quickly. For this reason, a sweep line algorithm usually comes along with some kind of efficient data structure such as B-trees or hash maps.

In Java you could use a java.util.HashMap (implemented internally using a hashing algorithm) and in C++ you could use STL’s map (implemented internally as an ordered tree) or use you own hashing algorithm. Given the tight time limit constraints for this problem (at least in the UVa judge), it’s probably better to use your own hashing algorithm. For a good introduction to many good hashing algorithms (and hashing in general), you can read this excellent article: The Art of Hashing.

I’d recommend you choose a simple algorithm, one that doesn’t perform many computations per byte. Some good ones are the Bernstein hash, the Shift-Add-XOR hash and the FNV hash. I personally use the FNV algorithm, but in practise they tend to perform very similarly.

I will not post the code for a hash table here because if you are about to write your own hash map implementation for the first time, I think it would be better to do it from scratch and use it as an exercise to learn the concepts in depth (and also you end up with something written in your own style). However, I’ll give you the general idea of how all of this glues together.

First, you have to implement your hash table. There are many ways to do it but a fairly simple and effective method is keeping a number of “buckets” to place your data into, and for any piece of data you want to store, you find its corresponding bucket using your hashing algorithm. The right amount of buckets to use depends on the problem, your hashing algorithm and the size of your input, but I’ve seen that you quickly reach a point where using more buckets doesn’t have any significant impact in the efficiency of your program, so you don’t need to choose a very big number. For this problem, for example, I’ve used \(2^{15}\). Since you have to assume that in general there will be collisions in your hashing procedure, each bucket is, in reality, a linked list (or vector) of data. Don’t worry if you think that using linked lists will be slow. When you have a fairly decent hashing algorithm, the number of collisions should be minimised, and the resulting average complexity is really good, perhaps even an order of magnitude better than using other data structures like trees in your buckets because of the minimal overhead of using a linked list or vector.

With your hash table in place, you apply the sweep line strategy. To put it all together, the algorithm for this problem could look something like this:

1. Read the data that describes the pool, and sort the hurdles, first by their mark \(p_i\), and then by their lane.
2. Let \(A=0\), where \(A\) represents our final answer.
3. Let \(R\) be the tuple \(\langle0, 0, 0\rangle\). Add \(R\) to your hash table, associated with the value 0 (the mark that corresponds to the tuple \(R\)).
4. Sweep line. For each hurdle in your data:
   1. Let \(m\) be the mark of the current hurdle. The tuple \(R_m\) is the same \(R\) we had previously, so calculate the difference \(d = m - \text{HT}(R)\) where \(\text{HT}(R)\) is the value associated to \(R\) in the hash table. Let \(A = \text{max}(A, d)\).
   2. Take from your input all other hurdles that are also at \(m\), and with that calculate \(R_{m+1}\).
   3. Add the new \(R\) to the hash table associated with the mark \(m+1\). If \(R\) was already in the table, calculate \(d = m + 1 - \text{HT}(R)\) and \(A = \text{max}(A, d)\).
5. In the end, the current \(R\) should be the value of \(R_L\), so calculate \(A = \text{max}(A, L - \text{HT}(R))\).

The final value of \(A\) should be our answer. Our resulting algorithm starts by sorting the input —with a complexity of \(O(n K \log{n K})\)— then does a sweep line (\(O(n)\)) with a hashing algorithm at each critical point (\(O(K)\)), which gives us an overall complexity of \(O(n K \log{n K})\).