Problem Name: Aladdin and the Magical Sticks
LightOJ ID: 1342
Keywords: math, probability, expected value, memoization, harmonic number
I’ve always had a keen interest in problems related to numbers, counting, probability and so on. It is only recently, however, that I’ve started to grow aware of the reasons why this might be so. Let’s take this problem as an example. After I read its description for the first time, I knew I would not rest until I found a satisfactory solution, and going into it I recognised that right then I still had some gaps in my knowledge, but still, it was thrilling to know that I was about to tackle something that would lead me to learn new things. It is a little hard to put into words, but there’s just something deeply enjoyable when you encounter a problem that you know you can’t yet solve, but your intuition tells you that you’re close; in other words, even if it’s a little beyond your current knowledge or skill, it’s within your reach. This is something that I’ve personally experienced with many math–related problems, and that’s probably the main reason why I find them fascinating.
Anyway, back to the subject at hand, this problem tells us the story of Aladdin, who is presented with a group of sticks, each one with a certain weight. He is asked to pick up the sticks, one by one, and every time he picks a stick, it is returned to the group and he has to continue picking sticks until all of them have been chosen. There’s a couple of extra details of importance: initially, the probability of picking any one stick is the same for all sticks, but, there’s also two types of sticks. One type is easily recognisable by Aladdin, so every time he picks a stick of this type, he doesn’t pick that same stick again. The other type of stick is normal and there is no way to recognise it, so sticks of this type could be picked many times. The question is: what is the expected weight of all the sticks Aladdin has to pick until all sticks have been chosen?
You may have noticed that this problem has a similar “flavour” to the Dangerous Maze problems —and they are, after all, from the same problem setter :). We could even rewrite the problem statement and use doors instead of sticks, and distances instead of weights, and the problems would look pretty similar. However, there is one crucial difference; in this problem you don’t “get out” until you have picked all sticks (or doors).
This difference turns this into an entirely different kind of problem. To give you some idea about the nature of the problems I’m talking about, think about how to calculate the expected number of throws of a single die until it shows a certain number, and how it differs from calculating the expected number of times you have to throw a die until you have seen all of its sides. Another way to look at it is to think about sticker albums or collectible card games. Let’s say that you can buy one card at a time, which comes completely at random (all cards with equal probability). How many cards do you need to buy until you complete your collection?
Not surprisingly, this is a classic conundrum known as the Coupon collector’s problem, and the math behind it is actually fairly accessible once you’re familiar with the basics of probability and expected value. Quoting from Wikipedia:
The key to solving the problem is understanding that it takes very little time to collect the first few coupons. On the other hand, it takes a long time to collect the last few coupons.
Let’s go back to the example with dice. Let’s say you want to know the expected amount of tosses until you have seen all sides from a standard die. You can split this problem into six sub–problems: how many tosses until you see the first “new” (previously unseen) side? How many tosses after that until you see the second “new” side? And so on until the sixth and final “new” side.
It’s easy to see that the first sides come up pretty quickly —you are guaranteed to see a new side on your first toss, and it’s very likely that you’ll see a new side on your second toss because the chance of repeating your previous toss is only \(1/6\). It’s the last unseen sides that take longer to come up. This leads to a very elegant formula for the expected value in the coupon collector’s problem. Using the terminology of this problem, if all sticks were of the second type (the type that is unrecognisable), then the expected amount of times that Aladdin would have to choose a stick until all of them were picked would be:
Where \(H_n\) is the \(n\)th harmonic number. At this point, I’d like to say that it’s very possible that you have now enough elements at your disposal to solve this problem. If you haven’t done so already, I suggest you take at least a couple of minutes right now to think about the mathematics of it, and try to formulate a solution —even a preliminary one. Nothing can replace that type of mental exercise.
Okay, now here’s what I found to be the final piece of the puzzle to arrive to my solution; it’s something I call “complementary” or “background–foreground” thinking (there’s probably a better name for it, but this is how I think of it). Edit: After re–reading some passages of one my favourite books ever —GEB— I can see that this concept is usually referred to as “Figure and Ground”. I’ll try to remember this…
Let me give you an example. Maybe you have confronted the Birthday paradox before, where you want to calculate the exact probability that any two people in a group of \(n\) people have the same birthday. You can approach this in two different ways, and one of them is going to be vastly easier than the other. You can try to go “straight” to the solution (what you see in the foreground) and consider every pair of people and the probability that they do have the same birthday. Obtaining the answer through this process is very complicated because of the relations formed between the pairs and the fact that you want to know the probability of any pair having the same birthday. The other approach is looking at the background or complement, and think of the probability that the \(n\) people have all different birthdays (let’s call it \(\bar{p}\)), and then your answer comes from the complement \(1 - \bar{p}(n)\). Much easier to calculate.
I hope the crux of the matter is clear. Sometimes if you can’t solve a problem looking at the foreground, it might be useful to look at the background and try to solve it from there. This is what I applied here. The idea is to initially consider all sticks as if they were of the second type; this gives us an initial expected weight \(W_i\). After that, subtract from \(W_i\) a weight from the sticks of type 1, proportionate to the “excess” in our calculation.
Why an “excess”? Well, it should be easy to see that if some of the sticks are of type 1, then our first estimation \(W_i\) is larger than the right answer, because no matter how we look at it, all sticks of type 1 are picked only once, no more. Let’s call \(\hat{E}\) the expected amount of times that one particular stick would be picked, if all sticks were of type 2. Then we have:
However, for sticks of type 1, this expected value is exceeded by the following amount (\(E_x\)):
Alright, now we can formulate the following algorithm:
- Let \(A_T\) be the average weight of all the sticks.
- Let \(E\) be the expected number of sticks that have to be picked (if all were of type 2). This comes directly from the coupon collector’s problem as \(E=n \cdot H_n\).
- \(W_i = A_T \cdot E\)
- If there is one or more sticks of type 1:
- Let \(N_1\) be the number of sticks of type 1 and \(A_1\) the average weight of the sticks of type 1.
- \(W_f = W_i - N_1(H_n - 1) \cdot A_1\)
- Else, \(W_f = W_i\)
Our answer is \(W_f\).
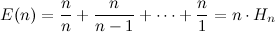
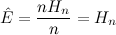
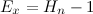
Please elaborate your idea behind this>>
ReplyDeleteHowever, for sticks of type 1, this expected value is exceeded by the following amount (Ex):
Ex=Hn-1
This comment has been removed by the author.
Delete