Problem Name: The Vindictive Coach
UVa ID: 702
LightOJ ID: 1173
Keywords: counting, dynamic programming
Isn’t it interesting how everything changes constantly, including ourselves, even without us noticing? I mention this because I was a little amused by the fact that I recently came back to this problem, which I tried to solve some time ago (unsuccessfully at the time, of course), but now the solution just popped in my mind almost immediately in a natural way. This is just very intriguing to me; how our minds work, and how things that some people may consider “difficult” seems genuinely “easy” to others and vice–versa, and how our conscious (and unconscious) learning modify these perceptions with time.
Anyway, let’s get back to this problem. It asks us to consider sequences formed by the first \(N\) positive integers, such that, starting with an arbitrary \(m\) (\(1 \leq m \leq N\)), it alternates between smaller and bigger numbers until all \(N\) integers have been used exactly once. The first number in the sequence has to be \(m\), then a smaller number must come next, then a bigger number, then smaller, and so on. For example, with \(N=5\) and \(m=3\) a valid sequence could be \(S_1=(3, 2, 5, 1, 4)\) but \(S_2=(3, 1, 4, 5, 2)\) and \(S_3=(3, 4, 1, 5, 2)\) would be invalid. In \(S_2\), after 4 there should be a smaller number, and in \(S_3\), the alternating sequence has to start by going “down”, so 4 can’t go second.
There is one special case that was a little confusing to me at first because of the wording from the problem statement. It happens when \(m=1\) (and only then). In that case, since it isn’t possible to start the sequence by going “down” to a smaller number, then it starts going up, but to the closest possible number that allows the zig-zag nature of the sequence to be maintained. In other words, if \(m=1\) and \(N>2\) then the second number of the sequence has to be 3, and then the sequence continues normally: \((1, 3, 2, \dots)\).
The question is simply, given the values of \(N\) and \(m\), how many valid sequences can be formed with the rules described? Now, it should be clear that at its core, this is a counting problem, where dynamic programming just happens to be a valid strategy to compute the answer easily. The trick is in formulating a relation that leads us to the answer.
Let’s generalise things a bit, and say that we have a list of \(k\) positive integers in ascending order, and we have just selected the \(i\)th element (\(1 \leq i \leq k\)) to be placed in the sequence. Now, the list has been split in two: there would be \(k - i\) elements left “above” our last selection (let’s call that group \(A\)), and \(i - 1\) elements “below” (we’ll call it \(B\)). Depending on the direction of our last movement (“up” or “down”), the next number would have to be selected from one of the two groups, \(A\) or \(B\). Let’s call \(a\) the number of elements in \(A\) and \(b\) the number of elements in \(B\). Let’s call \(n\) the last number added to the sequence so far.
To illustrate this a little bit better, let’s go back to the example \(N=5, m=3\). After picking the first number of the sequence, things would look like this:
\(A=(4, 5) \;;\; B=(1, 2) \;;\; a=2 \;;\; b=2 \;;\; n=3\)
We can now formulate the following:
- \(f(a, b)\)
- The number of sequences that can be formed from \(a\) numbers bigger than \(n\) and \(b\) numbers smaller than \(n\), where the next number has to be chosen from \(A\).
This takes care of our “up” movements, but we also need to handle the “down” case, so here’s the symmetrical \(g\):
- \(g(a, b)\)
- Similar to \(f\), but the next number has to be chosen from \(B\).
The base case would be when the number of elements to choose from is either zero or one:
Then the main D.P. relation would look something like this:
Let’s see how it works; let’s consider the \(f\) relation that describes the “up” movements —the reasoning for \(g\) is very similar. We have to select one number from the \(A\) group. We have \(a\) different choices for this next movement, and this is represented by \(f(a, b)\). If we choose the smallest number in that group, then we leave two groups: a new \(A\) with \(a'=a-1\) elements and \(B\) remains the same. If we choose instead the second smallest number, then the groups change in size as follows: \(a'=a-2\) and \(b'=b+1\) (because by choosing the second smallest number, the very smallest number moves into the \(B\) group). The same thing applies for the third smallest number, the fourth, and so on, and that’s what the summations represent.
Going back to our example \(N=5, m=3\), we know we have two options for the second number of the sequence: we can pick 1 or 2. If we picked 1, the new situation would be:
\(A=(2, 4, 5) \;;\; B=() \;;\; a=3 \;;\; b=0 \;;\; n=1\)
If we picked 2 instead, it would be:
\(A=(4, 5) \;;\; B=(1) \;;\; a=2 \;;\; b=1 \;;\; n=2\)
All of this information is for illustration purposes, but you can notice that the actual contents of \(A\) and \(B\), as well as the last number picked \(n\) are irrelevant. The only thing that matters in our algorithm is the values \(a\) and \(b\) and whether the next movement has to be “up” or “down”.
Notice also that this process is guaranteed to end at some point because the total number of elements used as arguments for \(f\) and \(g\) are being decreased by one at each step. This leaves us with an algorithm that can compute all possible answers in \(O(N^3)\). This is a pre–calculation that happens only once in the program, and then each test case can be answered in \(O(1)\). If \(m > 1\) then the answer would be \(g(N-m, m -1)\). The small adjustment for the case \(m=1\) is left as an exercise for the reader :).
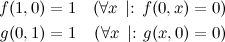
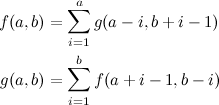
the problem also said that ,
ReplyDelete"Even in this case, the height difference should be as small as possible, while maintaining the zigzag arrangement of the line."
But you cannot discuss about this case..
It helps me a lot :) Thank you very much.
ReplyDelete