Problem Name: Tiles
LightOJ ID: 1244
Keywords: recursion, matrix exponentiation
This is a problem involving an interesting recurrence that combines different inter–dependent relations. Moreover, given the large range of the input, it can be tackled with matrix exponentiation instead of classic dynamic programming.
You have a rectangular board of size \(2 \times N\) that is to be filled with tiles of six different types. 2 tiles are formed by two squares (each of size \(1 \times 1\)) and have the shape of a bar. The remaining 4 tiles have three squares, representing the four different rotations of a L–shaped tile. The tiles have to be placed in the board as–is (without rotating or flipping them).
We’ll identify the six tiles by the characters \(A, B, \dots, F\). This is how they look, using a single lowercase character to represent each square:
a c dd e ff
a bb cc d ee fThe question is, in how many different ways can the board be filled using the six tiles?
It shouldn’t take long to see that it would be convenient to start by defining the following function:
- \(f(n)\)
- Number of ways to completely fill a board of size \(2 \times n\).
However, there is not a straightforward solution from just this relation —at least not one that I can see. Something that helps here is looking at a couple of additional “states” that can be analysed and used to build our final answer.
Consider the following auxiliary functions:
- \(g(n)\)
- Number of ways to fill a board of size \(2 \times (n-1)\), leaving a single square in the top row of the \(n\)th column.
and finally,
- \(h(n)\)
- Number of ways to fill a board of size \(2 \times (n-1)\), leaving a single square in the bottom row of the \(n\)th column.
Think for example of what happens when you have completely filled a section of the board of size \(2 \times k\), going from left to right, and you append a \(C\) tile. Then you have filled an area of \(2 \times (k+1)\), but you have an additional single square at the bottom of column \(k+2\). Those are the situations where \(g\) and \(h\) will prove useful.
Also, having these three relations make it possible to now formulate a definition of \(f(n)\):
These expressions come directly from thinking about the different ways to place the six tiles inside the board. Let’s take \(f(n)\) for example. By definition, \(f\) concerns itself only with filling the first \(n\) columns entirely, so it shouldn’t include cases where the tile \(C\) and \(D\) are placed last. It only considers the cases where the last tile is either: \(A\), represented by the term \(f(n-1)\); or \(B\), which leads to \(f(n-2)\) (using two \(B\) tiles one on top of the other); or \(E\) and \(F\), which lead to \(g(n-1)\) and \(h(n-1)\) respectively.
The definitions of \(g(n)\) and \(h(n)\) come from a similar reasoning. Try to deduce them by yourself thinking about the different ways in which you can leave one single square in the last column. The beauty of this is that now all the terms show recurrence and lend themselves to a matrix exponentiation strategy quite nicely.
Let’s outline two of the three matrices, leaving the matrix with the coefficients for last:
Now here’s the crucial step for our implementation. Given our previous definitions of \(f\), \(g\) and \(h\), we fill the matrix \(A\):
With this now we can write the implementation, and obtain the answer in \(O(k^3 log N)\), with \(k=4\).
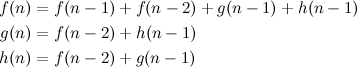
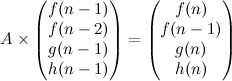
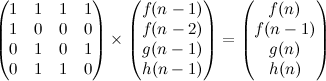
thanks a lot, great help.
ReplyDeleteThanks for this post. Can you post your code for this problem here, it will helps to understand it.
ReplyDelete