Problem Name: Olympic Swimming
UVa ID: 11546
LightOJ ID: 1423
Keywords: sweep line, hashing
The London 2012 Olympics closing ceremonies took place just a couple of days ago, and it has given me a nice excuse to work on a problem that somehow involves an Olympic event :). Actually, I had this problem near the front of my queue of “to do” problems and it coincidentally emerged during these days of “Olympics fever”. The real reason I find it noteworthy, however, is that it also gives me the opportunity to talk about a couple of interesting concepts that I have not talked about in previous posts.
The problem can be summarised as follows: imagine a swimming pool with length L metres (\(L \in \mathbb{Z}\)). This pool has K lanes, and marks at every metre, so you can imagine it as the sum of \(L\) sections, each one 1 metre long and with \(K\) lanes. The pool has a number of hurdles or obstacles (it doesn’t make much sense in real swimming events, but never mind that), such that each hurdle is placed on a particular lane, between two consecutive marks.
The question is, if you can divide the pool only at a mark, what is longest possible segment of the pool in which all the lanes have the same number of hurdles (not necessarily at the same locations)?
Let’s start by looking at an example to help us analyse this problem. Consider a pool of length 10 and with three lanes. The lanes will have 3, 4 and 2 hurdles, as depicted in the following figure:
Try to find two marks \((i, j)\) such that all lanes have the same amount of hurdles in that segment of the pool and \(j - i\) is maximised. After some trial and error, it should become clear that the longest segment is \((5, 9)\), with a length of 4 and one hurdle per lane.
Now we can discuss the first interesting concept that this problem leads us into, which is the sweep line algorithm. The idea behind this is simple (although the specific details for certain problems might not be simple at all): you have a geometric plane and a set of points that relate to your model of a problem; you use an imaginary line that is moved over the plane, and every time it hits one or more points, some type of calculation is performed. In this way you’re computing a certain value gradually with an algorithm that has, at first, a complexity of \(O(n)\) —not counting the operations you perform at each “collision”. This type of algorithm can be applied to many interesting geometry–related problems, like finding the closest pair of points in a set (see problem UVa 10245) or computing the outline of the union of a set of rectangles with a common baseline (see problem UVa 105).
We’ll apply the general principle to this problem, but first let us give it a little more thought and find out how a sweep–line strategy may be useful. One of the first things to notice is that if you start at the mark \(i=0\) and move forward all the way to \(i=L\), the number of hurdles at each lane can only increase or stay the same at each step, so maybe a prefix sum can help us get closer to the answer. Let’s start by defining the following:
- \(P_{i}\)
- A tuple with the prefix sums of hurdles at position \(i\). Each element in the tuple corresponds to one lane.
According to this definition, the values of \(P\) for our example are:
Do you notice anything particularly interesting in this list, keeping in mind that we know that our answer is in the segment \((5, 9)\)? You should see that the relative differences among the elements in \(P_5\) are the same as in \(P_9\). In fact, those two tuples form the pair that is the most distant while having the same relative differences internally. To see it more clearly, let’s bring a second definition that simplifies things for us:
- \(R_i\)
- A tuple where each element \(R_{i, j} = \text{max}(P_i) - P_{i, j}\)
Now we have enough elements to formulate our main algorithm. If we use a sweep–line, we could calculate \(R_i\) and \(R_{i+1}\) at each point \(i\) given in the input and every time we find an \(R\) tuple that we have seen before, we calculate the distance between the new mark and the old mark, and our final answer comes from choosing the overall maximum.
This brings us to the second concept that I want to talk about —hashing. You see, a sweep line by itself is just a very basic approach, but what’s important is the type of operations you do at each critical point you find in your sweep, which commonly requires keeping track of data (inserting, querying, deleting) very quickly. For this reason, a sweep line algorithm usually comes along with some kind of efficient data structure such as B-trees or hash maps.
In Java you could use a java.util.HashMap (implemented internally using a hashing algorithm) and in C++ you could use STL’s map (implemented internally as an ordered tree) or use you own hashing algorithm. Given the tight time limit constraints for this problem (at least in the UVa judge), it’s probably better to use your own hashing algorithm. For a good introduction to many good hashing algorithms (and hashing in general), you can read this excellent article: The Art of Hashing.
I’d recommend you choose a simple algorithm, one that doesn’t perform many computations per byte. Some good ones are the Bernstein hash, the Shift-Add-XOR hash and the FNV hash. I personally use the FNV algorithm, but in practise they tend to perform very similarly.
I will not post the code for a hash table here because if you are about to write your own hash map implementation for the first time, I think it would be better to do it from scratch and use it as an exercise to learn the concepts in depth (and also you end up with something written in your own style). However, I’ll give you the general idea of how all of this glues together.
First, you have to implement your hash table. There are many ways to do it but a fairly simple and effective method is keeping a number of “buckets” to place your data into, and for any piece of data you want to store, you find its corresponding bucket using your hashing algorithm. The right amount of buckets to use depends on the problem, your hashing algorithm and the size of your input, but I’ve seen that you quickly reach a point where using more buckets doesn’t have any significant impact in the efficiency of your program, so you don’t need to choose a very big number. For this problem, for example, I’ve used \(2^{15}\). Since you have to assume that in general there will be collisions in your hashing procedure, each bucket is, in reality, a linked list (or vector) of data. Don’t worry if you think that using linked lists will be slow. When you have a fairly decent hashing algorithm, the number of collisions should be minimised, and the resulting average complexity is really good, perhaps even an order of magnitude better than using other data structures like trees in your buckets because of the minimal overhead of using a linked list or vector.
With your hash table in place, you apply the sweep line strategy. To put it all together, the algorithm for this problem could look something like this:
- Read the data that describes the pool, and sort the hurdles, first by their mark \(p_i\), and then by their lane.
- Let \(A=0\), where \(A\) represents our final answer.
- Let \(R\) be the tuple \(\langle0, 0, 0\rangle\). Add \(R\) to your hash table, associated with the value 0 (the mark that corresponds to the tuple \(R\)).
- Sweep line. For each hurdle in your data:
- Let \(m\) be the mark of the current hurdle. The tuple \(R_m\) is the same \(R\) we had previously, so calculate the difference \(d = m - \text{HT}(R)\) where \(\text{HT}(R)\) is the value associated to \(R\) in the hash table. Let \(A = \text{max}(A, d)\).
- Take from your input all other hurdles that are also at \(m\), and with that calculate \(R_{m+1}\).
- Add the new \(R\) to the hash table associated with the mark \(m+1\). If \(R\) was already in the table, calculate \(d = m + 1 - \text{HT}(R)\) and \(A = \text{max}(A, d)\).
- In the end, the current \(R\) should be the value of \(R_L\), so calculate \(A = \text{max}(A, L - \text{HT}(R))\).
The final value of \(A\) should be our answer. Our resulting algorithm starts by sorting the input —with a complexity of \(O(n K \log{n K})\)— then does a sweep line (\(O(n)\)) with a hashing algorithm at each critical point (\(O(K)\)), which gives us an overall complexity of \(O(n K \log{n K})\).

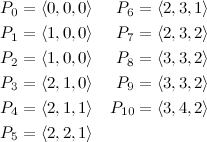
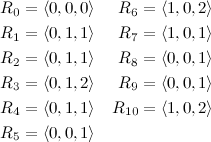
You are amazing Leonardo !!! The way you help people with their codes , you are an inspiration :-)
ReplyDeleteHi Art of hashing blog showing 500 could u post it if you have an idea about it.
ReplyDelete