Problem Name: Bubbles and Buckets
UVa ID: 11495
Keywords: sorting, inversion number
Since my previous post was about a problem that can be solved with a variation of a classic sorting algorithm, I thought it would be nice to do a follow–up with another problem that can also be solved by using a sorting algorithm as a basis.
In this problem it is said that two boys play a simple game: a random permutation of the first \(N\) positive integers is given, and then the two players take turns to make a move. A valid move consists of taking any pair of adjacent numbers that are in the wrong order (the first number is higher than the second), and swapping them. The player who can’t make a move (which means the list is completely sorted) loses. The question is, knowing the initial permutation, and the player who goes first, who wins?
Clearly, the core of this problem is finding the number of swaps between adjacent elements required to sort the list. If you don’t know how to find this value yet, take some time to look at the samples, and think about possible strategies to do it. You should be able to identify a few interesting invariants soon. For example: an indication of how far a number \(x_i\) is from its correct position is the amount of numbers larger than \(x_i\) that are located to its left, or the amount of numbers smaller than \(x_i\) that are located to its right. Let’s consider the first test case from the sample input:
In the table, \(\alpha\) represents the amount of numbers bigger than \(x_i\) that are left of the given number, and \(\beta\) is the amount of numbers smaller than \(x_i\) that are found to its right. As you can see, the sums from the \(\alpha\) and \(\beta\) rows are equal. That’s an invariant, and it’s related to the algorithm that we will ultimately use to calculate the answer.
Another way to look at it is this: \(\alpha\) and \(\beta\) are the amount of swaps that every number has to go through to sort the list. \(\alpha\) corresponds to swaps from right to left, and \(\beta\) to swaps from left to right. No matter the orientation of the swaps you choose, the total number of swaps will always be the same. In discrete mathematics, this is also known as the inversion number of a sequence.
Now, how to calculate this efficiently? Note that there can be up to \(10^5\) numbers in the list, so any kind of \(O(n^2)\) algorithm wouldn’t work. Well, we can just choose any of the \(O(n \log{n})\) sorting algorithms and adapt it to keep track of the number of times a swap in one particular direction has to be performed. One particularly good alternative is merge sort because of its simplicity, in contrast to something like quick sort, where —depending on your implementation and the way you handle the pivot— figuring out the number of swaps required when a number has to change its place can be significantly harder.
Having settled on the algorithm to use, let’s see an example of the implementation of merge sort for this problem:
typedef long long i64;
typedef vector<int> IV;
typedef IV::iterator IVi;
i64 n_swaps; // the number of swaps can be very large
// auxiliary function used by merge_sort
void merge(IVi lo, IVi hi, IVi mid)
{
IV x;
for (IVi a = lo, b = mid; a < mid || b < hi; ) {
if (a >= mid) { x.push_back(*b++); continue; }
if (b >= hi) { x.push_back(*a++); continue; }
if (*a < *b) { x.push_back(*a++); continue; }
x.push_back(*b++);
// here is the problem-specific adjustment
// what does (mid - a) correspond to?
n_swaps += mid - a;
}
for (IVi a = lo, b = x.begin(); a < hi; ++a, ++b)
*a = *b;
}
// merge sort algorithm, receives iterators to the first (inclusive)
// and last (exclusive) elements of the range to sort
void merge_sort(IVi lo, IVi hi)
{
if (hi <= lo + 1) return;
IVi mid = lo + ((hi - lo) / 2);
merge_sort(lo, mid);
merge_sort(mid, hi);
merge(lo, hi, mid);
}
For a similar problem —the algorithm is exactly the same, the main difference is that you have to print the number of swaps— see the problem Ultra-QuickSort (UVa ID 10810). Another similar problem, but with lower constraints (enough to make a \(O(n^2)\) solution feasible) is Flip Sort (UVa ID 10327).
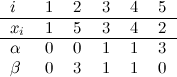
No comments:
Post a Comment