Problem Name: Baker Vai
LightOJ ID: 1071
Keywords: dynamic programming
One thing that I have heard and read numerous times about dynamic programming, and I completely agree with this, is that no matter how much experience you have solving problems using D.P., there’s always the chance that a new problem shows up that makes you stop and think hard about how to solve it. When that happens, it’s a beautiful thing, because you get the chance to expand the problem solving framework in your mind a little bit and get new inspirations on how to tackle problems in the future.
I liked this problem because it was one of those cases for me. The problem asks for the maximum sum possible when moving inside a matrix of integers of size \(m \times n\). You start on the top-left corner, and moving only down or right you have to reach the bottom-right corner, and then go back to where you started, moving only up or left. In addition, you can’t step on any cell more than once, except for the point where you started.
One thing that usually helps is trying to model the problem as something “simpler”, but equivalent (simpler is, of course, a matter of perception and it works differently for different people). Here’s how I thought about this; consider a matrix of size \(m \times n\):
The problem is equivalent to finding two disjoint paths \(P_L\) and \(P_R\) (representing a left path and a right path), such that \(P_L\) starts at position \((1,1)\) and ends at \((m,n-1)\), and \(P_R\) starts at \((1,2)\) and ends at \((m,n)\):
The paths have to be built with only two kinds of movement, right or down, and the sums of the cells they visit have to be maximum. Can you see how this is equivalent to our original problem?
There are a few interesting invariants that apply to this model, very similar to the ones that apply to the easier problem of solving this just for one path. For example, both \(P_L\) and \(P_R\) will have exactly \((m-1)\) down movements and \((n-2)\) right movements.
Let’s try to define our D.P. relation now:
- \(F(i, j, k)\)
- The maximum sum possible after reaching the \(i\)th row, where \(P_L\) is on column \(j\), and \(P_R\) is on column \(k\).
The base case is the first row:
Now, for the rest of the rows, we’ll consider three cases: both paths go down one step at the same time, or \(P_L\) moves to the right, or \(P_R\) moves to the right:
Note that the expression in the line marked with (*) has a special caveat: it can only be considered if \(x_{i j}\) is not part of \(P_R\). Otherwise, you may count some cells twice, and that would produce the wrong results.
For example, consider the following pseudo-code for the above relation:
dp[M][N][N] is the D.P. data structure
for each i from 2 to M:
for each j from 1 to N-1:
for each k from j+1 to N:
// calculate the new DP value
val := dp[i-1][j][k] + x[i][j] + x[i][k] ;
val := max(val, dp[i][j][k-1] + x[i][k]) ;
val := max(val, dp[i][j-1][k] + x[i][j]) ;
dp[i][j][k] := val ;
end for;
end for ;
end for ;
This code has the bug of not taking into account the caveat mentioned above. The order in which the columns \(j\) and \(k\) are visited by the loops don’t guarantee that x[i][j] hasn’t been counted already for dp[i][j][k-1].
How to fix it? Well, you can think about it like this: imagine that you use a chessboard of size \(m \times n\), and place two pawns in positions \((1,1)\) and \((1,2)\), and with them you simulate the movements of \(P_L\) and \(P_R\). One way to guarantee a correct sequence of movements is this:
- Let’s say that the two pawns are on row \(i\), and columns \(j\) and \(k\). First, move only the left pawn (the one at column \(j\)) to the right a certain number of times (but its final column has to be less than \(k\)).
- Then move only the right pawn to the right, any number of times (without going out of the board).
- Finally, if \(i < m\), move the two pawns down and go back to the first step.
That’s it. The way to avoid the counting cells more than once problem is in the order of our calculations.
The following pseudo-code illustrates a correct way of calculating the D.P. values for the rows 2 to \(m\):
for each i from 2 to M:
// First consider only the down movement
for each j from 1 to N-1:
for each k from j+1 to N:
dp[i][j][k] := dp[i-1][j][k] + x[i][j] + x[i][k] ;
end for;
end for ;
// Now, move the left path only
for each j from 2 to N-1:
for each k from j+1 to N:
dp[i][j][k] := max(dp[i][j][k], dp[i][j-1][k] + x[i][j] ;
end for;
end for ;
// Finally, move the right path only
for each j from 1 to N-2:
for each k from j+2 to N:
dp[i][j][k] := max(dp[i][j][k], dp[i][j][k-1] + x[i][k] ;
end for;
end for ;
end for ;
Note how in this pseudo–code, the indices for the D.P. matrix go from 1 to M and 1 to N, and how the loops are slightly different according to the situation.


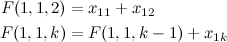
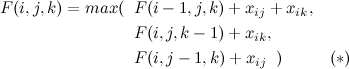
Superb explanation, you just made it look simpler :)
ReplyDeleteThank you very much. I think I got it.
ReplyDeletegood explanation
ReplyDeleteThanks a lot for this good explanation.
ReplyDelete