Problem Name: Aladdin and the Optimal Invitation
LightOJ ID: 1349
Keywords: math, median, sorting, recursion, quickselect
Sometimes you come across a problem that forces you to look into new, interesting algorithms, which is always an excellent opportunity to extend your bag of tricks as a programmer, and can give you a new level of understanding of classic algorithms you take for granted. This problem is a good example.
You are given a rectangular matrix of integers, representing a town, where the integer values of each cell represent the amount of people living on that cell. You are asked for a particular position inside the matrix, such that the total sum of Manhattan distances of all people relative to that position is minimised. One thing you can quickly notice is that in this 2D problem you can consider each axis independently and combine the horizontal and vertical cases for your final answer.
Now, let’s think abstractly about the problem in one dimension; that is, given a set of 1-dimensional coordinates, find an optimal coordinate such that the total sum of distances from each point of the set to that optimal position is minimal. If you have come across this type of problem before, you probably know already that the answer is the median of the set of points. In case it’s not clear why, let’s stop for a moment and try to find a satisfying explanation:
Let’s express the total sum of distances of all the points in the set to an arbitrary position \(x\) as a function:
Where \(p_i\) is each point from the set, and \(n\) is the number of points. Now, doing some mathematical optimisation, we find the first derivative of \(f\):
Where \(A\) is the number of points above \(x\), and \(B\) is the number of points below \(x\). The function \(f\) is minimal when its first derivative equals zero, which happens when the amount of points above \(x\) is the same amount of points below \(x\), or, in other words, when \(x\) is the median of the set of points. Note that there could be more than one value of \(x\) that satisfies the relation, which is consistent with the fact that the median is ambiguous when the number of points is an even number.
Solving this type of problem for relatively small data samples is very straightforward, just store the points in a list, sort the list, and find the value in the middle. For an example of a programming problem that can be solved this way, see Vito’s Family (UVa ID 10041). However, the constraints in this problem make it impossible to solve it with that approach. There can be \(5 \times 10^4\) populated cells in the matrix, and a maximum of \(10^4\) people can live on each cell.
One way to solve this is using an algorithm known as “quick select”. A good explanation on this algorithm can be found here: Selection and order statistics. You don’t have to read the whole article, but at least make sure to glance over the “Quick select” and “Analysis of quickselect” sections.
You can think about it as a variation of the standard quick sort algorithm. In quick sort you receive a list of values, choose one of them as a pivot and then partition the list into three groups: the values to the “left” of the pivot, the values to the “right” of the pivot, and the pivot itself. If any of the left of right groups is not empty, you then call quick sort recursively on them. Quick select is very similar, but the difference is that its purpose is not sorting the list, but finding an arbitrary element in the list (let’s call it the \(k\)th position).
So the algorithm chooses a pivot (just like quicksort), partitions the list, but then it simply does the following checks:
- If the left group has at least \(k\) elements, then the \(k\)th element must be found there, so call quickselect recursively on that group.
- If the pivot is exactly the \(k\)th element, then the pivot has to be returned.
- Otherwise, the answer must be found on the right group, so make the recursive call on that.
In a way, this algorithm is simpler than quick sort because it doesn’t need to make recursive calls for the groups where it knows that the \(k\)th element is not going to be found. With all of this in mind, now let’s see a C++ implementation of quick select specifically tailored for this problem, heavily based on the pseudo-code for the “in-place” version of quick sort from Wikipedia.
struct Data {
int v; // value of data point (one-dimensional coordinate)
int n; // number of occurrences (people on that coordinate)
int p; // a sequential number, to break ties
Data(int V, int N, int P) : v(V), n(N), p(P) {}
bool operator<(const Data &x) const {
if (v != x.v) return v < x.v;
if (n != x.n) return n < x.n;
return p < x.p;
}
};
// we will use STL's vector
typedef vector<Data> DV;
typedef DV::iterator DVi;
/**
* Selects an arbitrary position from a range of data, according
* to its logical order. It modifies the vector in-place.
*
* @param lo The iterator to the first element in the range (inclusive)
* @param hi The iterator to the last element (exclusive)
* @param k Index of the element to return (starting with 0)
*
* @return The kth element in order from the range of data
*/
int select_kth(DVi lo, DVi hi, int k)
{
// if there is only one element left, it must be the answer
if (hi == lo + 1) return lo->v;
// choose a pivot at random
int pivot_index = rand() % (hi - lo);
// move the pivot to the last position
swap(*(lo + pivot_index), *(hi - 1));
// keep the pivot's value at hand
Data piv = *(hi - 1);
// iterator to keep track of the "left" group
DVi x = lo;
// number of people that has gone to the "left" group
int lt = 0;
// traverse the range of data
for (DVi i = lo; i < hi - 1; ++i)
if (*i < piv) {
// if the current element belongs to the left group ..
swap(*i, *x); // move it to the tail pointed by x
lt += x->n; // increase the number of people
++x; // move the x iterator
}
// move the pivot back to its rightful place
swap(*x, *(hi - 1));
// if k is found in the left group
if (k < lt)
return select_kth(lo, x, k);
// if k is greater than the amount of people in the left group
// and the pivot
if (k >= lt + x->n)
return select_kth(x + 1, hi, k - lt - x->n);
// the only possibility now is that k is in the pivot
return x->v;
}
As you can see, it follows the quick sort pattern very closely, but it doesn’t bother sorting the entire list, just locates the \(k\)th element.
A couple of details are worth noting: the use of an extra field (p) in the Data structure (line 4), and the selection of the pivot at random (line 35). Both are related to the same issue: performance. If you read the comments on the performance of this algorithm in the article cited above, you realise that it can have a \(O(n^2)\) complexity for a worst case, but it is asymptotically optimal if the pivots are chosen carefully.
I actually came across this issue while testing my solution. Consider a test case with \(q=50000\), where \(u\) and \(v\) are always the same, and \(w\) is always \(10000\). If we always choose the pivot to be, let’s say the first element of the range, then it’s clear that on each call of the select_kth function the “left” group will be empty, and it will keep calling itself after discarding only one element from the list (the pivot). Clearly in this case it will perform very badly.
However, by always choosing the pivot randomly, and by making sure that the Data points can always be sorted unambiguously, the “left” groups will be of an average size, and the total complexity gets reduced drastically.
I really liked how this problem shows that, even if you would very rarely need to write a quick sort function (using the implementation from your programming language is a much better idea), knowing its inner workings is very useful to implement variations like quick select, which has the potential to provide elegant solutions in problems related to selecting elements from large lists.
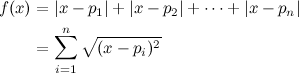
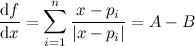
No comments:
Post a Comment