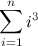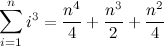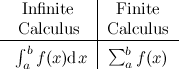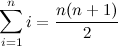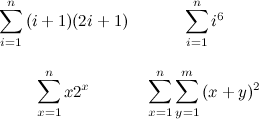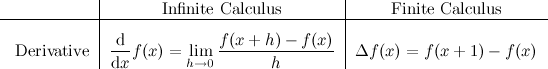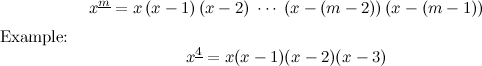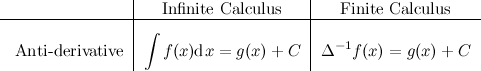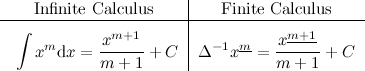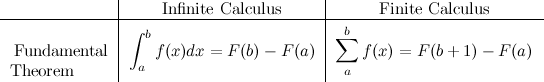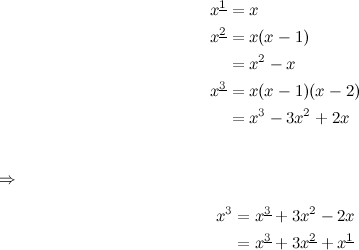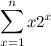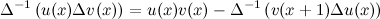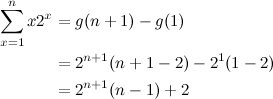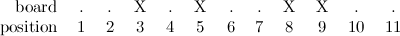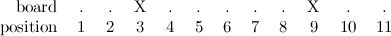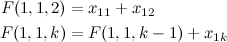Problem Name: Summation of Polynomials
UVa ID: 10302
Keywords: finite calculus, math
I have a real treat for you today. I am thrilled to have the opportunity to write about a fascinating topic I just learned about very recently. This post is supposed to be about problem 10302 from UVa’s archives, but it’s not simply about the specific solution to the problem, which is rather mundane, but about the theory behind it, which is introduced in the problem description.
It all started when I read this problem for the first time. If you haven’t done so yet, I suggest you go ahead and read it now. Read it a few times if necessary…
Ready? Okay, did you find anything particularly interesting there? If you managed to perfectly understand all that is being said there, I salute you, you are a true gentleman and a scholar. Personally, I found the problem description quite confusing, and the subtle errors (did you notice something funny in the definition of a factorial polynomial?) didn’t help. However, the concepts being described there had some strange appeal to me, so it motivated me to do some research on my own. I’m so glad I did! It allowed me to learn about this beautiful area of mathematics that you could call finite calculus (or discrete calculus).
Before going any further, let’s quickly mention that the solution to this problem involves simply calculating the expression:
A simple search for “sum of consecutive powers” brings up countless documents that present the closed form expression to evaluate this sum:
We’ll come back to this later; for now, let’s go on with the topic at hand.
Finite Calculus - Calculus for computer scientists
Of course, people could disagree with this, but it seems to me that if you have any interest at all in computer science, there’s a good chance that you’ll find finite calculus deeply fascinating. For me, this was another instance of something that made me think “why didn’t they teach me this in school?!”. Maybe finite calculus is nothing new to you, and if that is the case, this post will be kind of boring, but if your academic education was somewhat similar to mine, you learned about the “traditional” branches of calculus: differential and integral calculus —which we’ll simply refer to as “infinite calculus” from here on— but you never heard about finite calculus.
Well, I’m not claiming that this article will teach you everything there is to know about it, but it may be a good starting point. Let’s start with the basics; as their names suggest, infinite calculus and finite calculus are sub-fields of Calculus, but they differ in a very fundamental way. Infinite calculus concerns itself with curves, sums of infinite terms and functions that exist in the realm of the real numbers, while finite calculus is more interested in sequences, sums of a finite number of terms and functions that live in the space of integers. The following figure oversimplifies things, but illustrates the kind of things that each type of calculus focus on:
One of the most emblematic examples of a function relevant to our discussion that shows up frequently in computer science and discrete mathematics in general is the sum of the first \(n\) positive integers:
In fact, I’d say that if you’re reading these lines, it’s very likely that you already know the equation above by heart (and, maybe just as likely, you have heard the charming story about young Gauss and how he amazed his teacher by using a brilliant reasoning related to that formula). However, can you say that you are equally capable of formulating closed form expressions for the following sums, without any help from books or other sources?
Well, if you are currently unable to answer affirmatively, rejoice, because you’re about to learn a nice approach to tackle these problems. I want to emphasize that this article is meant to be a simple introduction to finite calculus, but you can find a more complete document in the tutorial referenced at the end. I strongly recommend that you read it in its entirety for a more detailed explanation on many of the things mentioned here.
Definitions
Let’s get started (about time!). What we’ll see here is how, even though the basic definitions in finite calculus are necessarily different than the things you already know from infinite calculus, they closely relate to their infinite counterparts. Because of this, if you already know the basics of infinite calculus, learning finite calculus will be a breeze.
We’ll begin with the discrete derivative:
In discrete mathematics, the closest we can get to 0 (from the right) without touching it is 1, which gives us the simple expression above. \(\Delta\) is the finite difference operator, which in this case simply represents the difference between the value of a function evaluated at some point \(x\), and its value when evaluated one step above \(x\). This should give you an idea as to why the problem description talks about “anti-differences”, and why its definition looks the way it does.
Next, let’s see one of the most basic operations which we’ll use repeatedly from now on, the exponentiation or “power” function:
What is \(x^\underline{m}\)? It’s a “falling power” (the problem description calls it a factorial polynomial):
Why use such a strange type of “power”? Well, it will become clear when you see how the “derivatives” of polynomials work in finite calculus:
Isn’t that neat? Now that we have covered the basic of “finite differential calculus”, let’s see a little bit of “finite integral calculus”, which is what we’ll ultimately apply to solve the summations formulated above.
A function \(g(x)\) is called the discrete anti-derivative, or anti-difference of \(f(x)\) if \(\Delta g(x) = f(x)\):
Here I have chosen \(\Delta^{-1}\) to denote the discrete anti–derivative. A different notation is used in the tutorial referenced at the end, but the meaning is the same. Notice that the similarities with infinite calculus still hold:
The last crucial element is to formulate something similar to the fundamental theorem of calculus, but for the discrete world:
Where \(F(x)\) represents the anti–derivative of \(f(x)\). All of these elements give use enough tools to tackle our original problem, but before moving on to the examples, I want to mention a few more properties and relations that have elegant discrete counterparts (click on the image).
I find particularly interesting that the discrete counterpart of \(e\) is 2. If you are into computer science, I don’t need to explain how perfect that is.
Worked Example #1
Okay, let’s try applying all of this theory in a real problem. Let’s get back to our original summation:
How to solve this? Well, the fundamental theorem tells us that if we knew the anti–difference of \(x^3\) (let’s call it \(g(x)\)), then calculating the sum would be a matter of evaluating \(g(n+1) - g(1)\).
But to find \(g(x)\), first it would be convenient if we could express \(x^3\) as a sum of falling powers (a factorial polynomial):
With this, finding the anti–difference is very easy:
Verifying that \(g(n+1)-g(1)\) is equal to the closed form formula presented at the beginning of this article is left as an exercise to the reader.
Worked Example #2
We’ll consider now the following summation (taken from the tutorial referenced below), which illustrates the use of “integration by parts” in finite calculus:
The key observation here is that, thanks to the multiplication of derivatives property, we can formulate the following relation —again, notice the striking similarity with infinite calculus:
We’ll choose \(u(x)=x\) and \(\Delta v(x)=2^x\), which helps us find the anti–difference we want:
Finding the closed form expression for the sum is now trivial:
Really nice, isn’t it?
We have reached the end of this short introduction to the world of discrete calculus, and all that is left for me is to thank the problem setter for writing this problem specifically to introduce many of us to these fascinating mathematical ideas. See? This is one of the reasons why I love solving algorithm problems; every once in a while you come across a gem like this that helps you learn new and exciting stuff, and isn’t learning the point of all this? :)
References
- David Gleich. Finite Calculus: A Tutorial for Solving Nasty Sums. 2005.
http://www.cs.purdue.edu/homes/dgleich/publications/finite-calculus.pdf