Problem Name: Winning Streak
UVa ID: 11176
Keywords: dynamic programming, probability, expected value
This is a very nice problem that involves probability and dynamic programming. What I find particularly nice about it is that formulating the D.P. structure requires, I think, a little creativity.
First, it’s necessary to understand how the expected value is calculated, and how are the probabilities of separate events combined to produce the probability that all events occur.
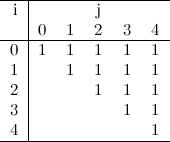
With that out of the way, and after some time pondering on how to model this problem for a D.P. solution, we could initially define the relation \(f(i, j)\) as follows:
- \(f(i, j)\)
- The probability of having a winning streak of exactly \(j\), after \(i\) games.
However, it is more convenient to define it slightly different, for reasons that will become apparent in the reasoning below:
- \(f(i, j)\)
- The probability of having a winning streak of \(j\) or less, after \(i\) games.
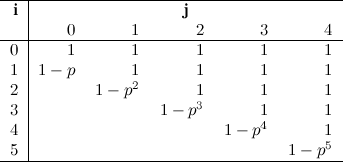
For example, \(f(5, 3)\) would be the probability of having a winning streak of 0, 1, 2 or 3 after 5 consecutive games. Then we can begin to see how our D.P. data structure will be filled. First of all, for all pairs \((i, j)\) where \(j \geq i\), it’s easy to see that the probability is 1:
Now, when \(j = i-1\), the value of \(f(i,j)\) will be \((1 - p^i)\), where \(p\) is the probability of winning a game. This is because the only way to have a winning streak of \(i\) in \(i\) games is winning them all in a row (hence the \(p^i\)), and that is the only case that need to be excluded from \(f(i, i - 1)\).
We have now:
For the remaining positions (\(j < i-1\)), we need to figure a way to calculate their values, relating it to what we already have. Let’s compare the meaning of \(f(i, j)\) and \(f(i-1, j)\).
When we think about \(f(i-1, j)\), we recognise that it corresponds to the probability of the sequences of games:
Where \(G_k\) for all \(k\) between 1 and \(i-1\) is either W or L, and where there are at most \(j\) consecutive W’s. Similarly, \(f(i, j)\) is the sequence:
Where there are also at most \(j\) consecutive W’s. Let’s consider what is happening with \(G_i\). It could be L, in which case nothing changes, because it doesn’t create any winning streak bigger than \(j\). Or it could be W, and in that case, we need to remove those cases where it does create a winning streak of \(j+1\).
Given that we can be sure that in the sequence up to \(G_{i-1}\) there are at most \(j\) consecutive W’s, then the only way for \(G_i\) to create a winning streak of \(j+1\) is this:
And so, we reach to the formula for our remaining positions (where \(j < i-1\)):
To get our answer we just need to iterate over the nth row of our data structure, and use the fact that \(f(n, j) - f(n, j-1)\) is the probability of having a winning streak of exactly \(j\) in \(n\) games.
Our final implementation in code then could look something like this:
// dp[i][j] will have the probability of having a maximum winning streak of
// j in i consecutive games
double dp[MAXN + 1][MAXN + 1];
// pp[i] will have p^i
double pp[MAXN + 1];
int n; // from the input, the number of consecutive games
double p; // from the input, the probability of winning 1 game
double ans;
void run_dp()
{
pp[0] = 1.0;
for (int i = 1; i <= n; ++i) pp[i] = pp[i - 1] * p;
for (int j = 0; j <= n; ++j)
dp[0][j] = 1.0;
for (int i = 1; i <= n; ++i)
for (int j = 0; j <= n; ++j) {
dp[i][j] = dp[i-1][j];
if (j == i - 1)
dp[i][j] -= pp[i];
else if (j < i - 1)
dp[i][j] -= dp[i - j - 2][j] * (1-p) * pp[j+1];
}
ans = 0.0;
for (int j = 1; j <= n; ++j)
ans += j * (dp[n][j] - dp[n][j - 1]);
}
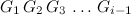
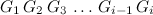

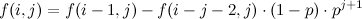
No comments:
Post a Comment