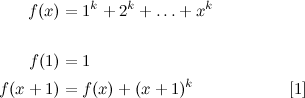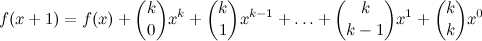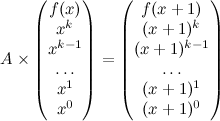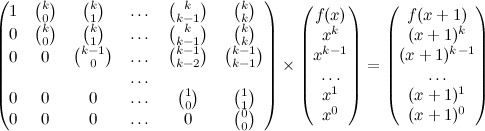Problem name: Summing Up Powers
LightOJ ID: 1132
Keywords: matrix exponentiation
This is a Matrix Exponentiation problem. With M.E., as is the case with many other concepts (like D.P.), I think it’s one thing to understand the fundamental idea, which is relatively easy and takes little time, and then another thing is developing your skills to apply the idea in different situations, which is a never-ending process.
For the first part, there is some good material on the web, like this article by Zobayer :). For the second part, it’s mostly a matter of practising. I’ll try explaining how I modelled this problem, but there are probably other ways.
Basically, the usual way to recognise if a problem can be solved by M.E. is if it involves a recurrence relation, and its constraints are too large for a D.P. solution. More specifically, if we can express the recurrence relation as a function \(f\), that depends on a set of functions \(g_1, g_2, \dots, g_k\), and a set of coefficients \(a_1, a_2, \dots, a_k\):
If all the \(g_i\) functions are also recurrence relations which can be deduced from known elements, then you’re all set! You just need to fill three matrices \(A, B, C\), such that \(A \times B = C\). The \(B\) matrix has size \(k \times 1\), and is filled the expressions \(g_1(x), g_2(x), \dots, g_k(x)\). The \(C\) matrix is also \(k \times 1\), and is filled with \(g_1(x+1), g_2(x+1), \dots, g_k(x+1)\), and the matrix \(A\) (size \(k \times k\)) is filled with coefficients that are easy to determine using \(a_1, a_2, \dots, a_k\), and the fact that the expression \(A \times B = C\) needs to evaluate to true. By the way, I’m not a mathematician and I could be abusing the language around here, but I hope the main idea is clear :).
Now, let’s try to apply all this to this problem. A first attempt to express the function as a recurrence relation can be like this:
Now, from the right hand of [1], we can see that \(f(x)\) is a recurrence relation, and \(f(x+1)\) is already defined from known expressions. What is not so apparent, is the second expression. How to calculate \((x+2)^k\) from the expressions we have?
We’ll, let’s start by expanding the expression. Thanks to Pascal’s triangle, we know that expanding the binomial \((x+1)^k\) produces the following:
This looks better. Now we have a set of binomial coefficients, and a set of expressions of the form \(x^i\), which have recurrence, meaning that we could calculate \((x+1)^i\) using the expressions we have already.
Now let’s put this in matrix form. Let’s begin with \(B\) and \(C\):
And knowing what we know, fill the matrix of coefficients:
There you go. To complete the solution, all the binomial coefficients could be pre–calculated, and then simple matrix operations would produce the result in \(O(k^3 \log{x})\). Really impressive!